Parallel Programming in Haskell

When executing multiple tasks there are essentially two different paradigms: concurrent programming, which switches between tasks on a single thread:

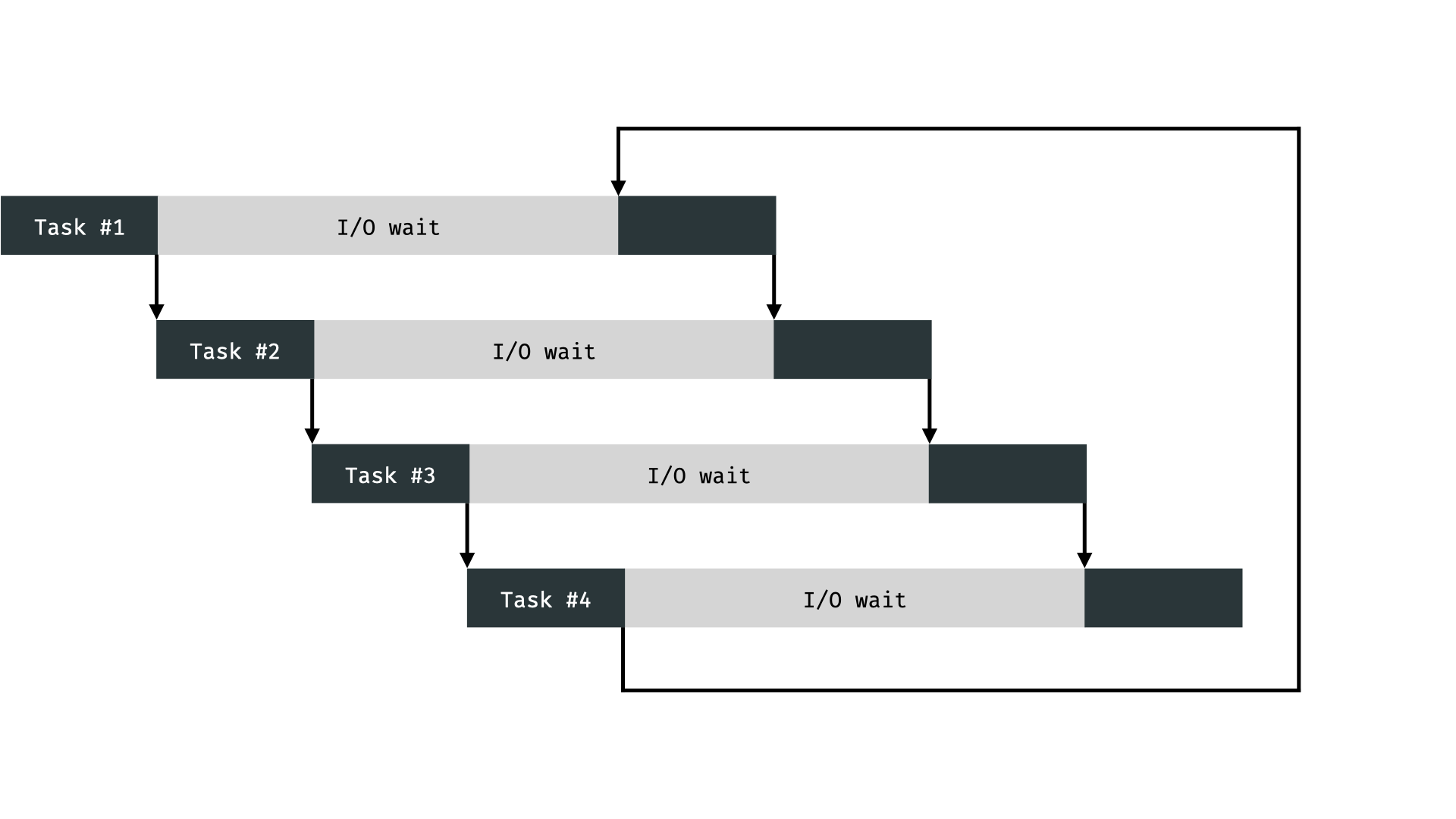
and parallel programming which deals with multiple processors executing things at the same time:

Large parts of this lecture are based on chapter 2 of the book Parallel and Concurrent Programming in Haskell by Simon Marlow.

Much of the motivation for non-mutating, lazy, functional programming languages comes from the promise of easier parallelism. So, what do we actually gain from all the hoops that we are jumping through while we are programming Haskell code?

• Parallel programs in Haskell are deterministic! No parallel debugging needed! No race conditions, no deadlocks! This is possible because we only have pure, non-mutating functions in Haskell.
• High-level declarations of parallelism via rpar and rseq. No syncronization/communication code needed! This is possible because Haskell is lazy and we only have to choose a reasonably smart startegy of evaluating expressions/thunks.

When writing parallel programs we mostly just have to think about

• The granularity of how we divide up our tasks to achieve maximal performance. If we make chunks of our problem too small, managing tasks outweighs the benefit of parallelism, if we make them too large, not all processors will be working at all times.
• Data dependencies of our tasks. If one bit of our problem depends on a previous bit, we have to wait for the former.

You will see that (at least theoretically) parallelizing a Haskell program can be incredibly simple once we have understood a few key points and primitives of parallel evaluation strategies.

Install System.Parallel.Strategies

# install ghcup on your OS

ghcup install latest
ghcup set latest
ghcup install cabal

cabal install --lib parallel

Evaluation

Haskell is lazy, so the expressions that we write are not evaluated until the are needed. For example, we can define a map over a list, but as long as we do not print it, it will not be evaluated. We can investigate this by using :sprint, which prints an expression without evaluating it. Below _ indicates: unevaluated.

𝝺> xs = map (+1) [1,2,3,4,5,6] :: [Int]
𝝺> :sprint xs
xs = _

If we compute e.g. the length of this list we need to know how many elements it contains, but the elements itself do not matter for the length, so Haskell does not evaluate them:

𝝺> length xs
6

𝝺> :sprint xs
xs = [_,_,_,_,_,_]

We can explicitly force evaluation to the first constructor by using seq:

𝝺> xs = map (+1) [1,2,3,4,5,6] :: [Int]
𝝺> :sprint xs
xs = _

𝝺> seq xs ()
()

𝝺> :sprint xs
_ : _

where seq evaluates the first argument and returns the second. We can see that the list is only evaluated to the first cons : and no further.

WHNF

The evaluation to the first constructor is also called weak head normal form (WHNF). For complete evaluation you can use deepseq, but we will not need this today.

Work stealing queue

GHC's strategy to evaluate thunks is based on a work stealing queue (see also this blog about the GHC scheduler). We can tell Haskell to create sparks, which essentially are just pointers to thunks that are put on a queue to be executed in parallel. Given a bunch of thunks that you want to run in parallel, GHC will do the following:

1. Create one work stealing queue per available processor (can have multiple threads).
2. Put all sparks on the work stealing queue on the main process.
3. All other processes are idle, so they can look for work, which means they try to steal sparks from the back of the queue of other processors.
4. Processors with a non-empty queue will pop of sparks from the front of the queue and evalute them.

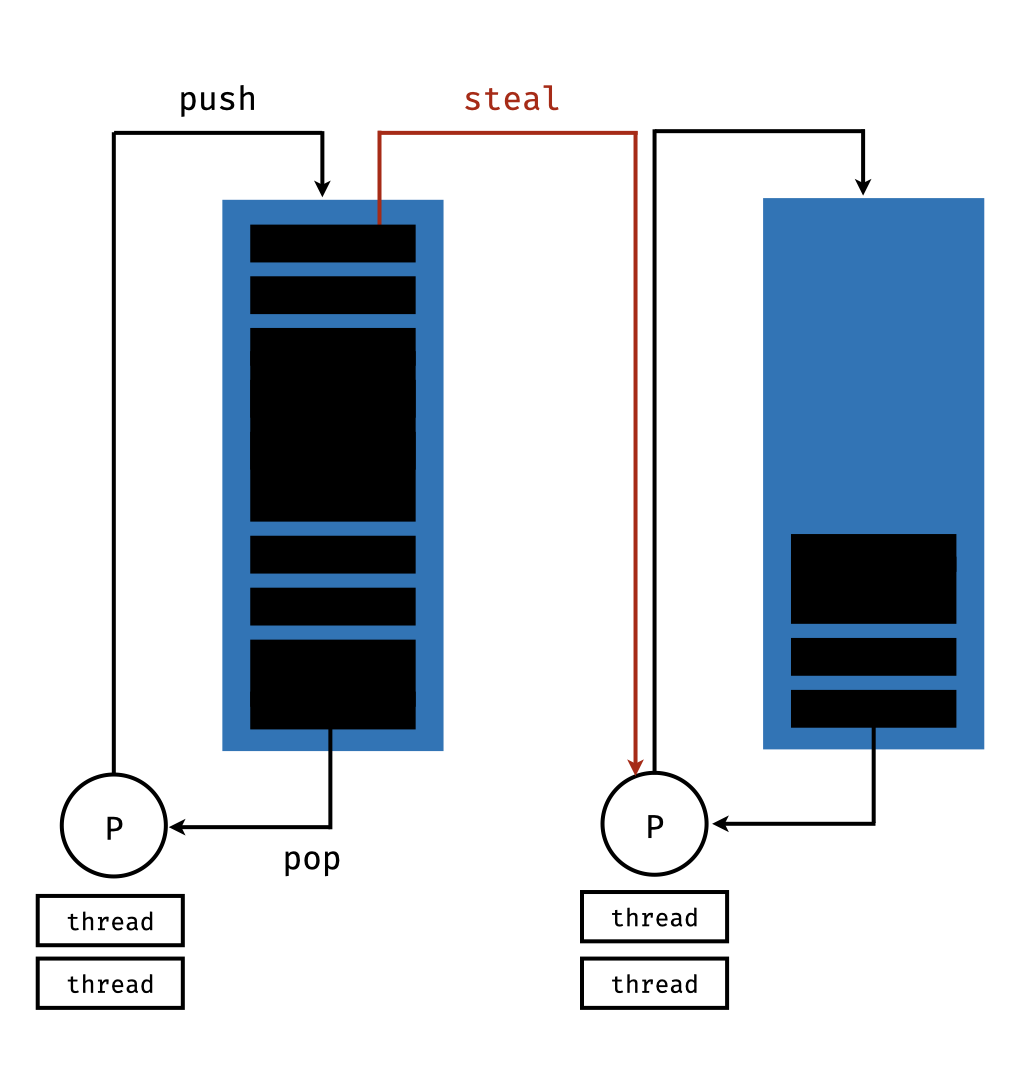
Advantages of this approach:

• The main thread does not have to sync with anyone, it can just take things from its own queue.
• Idle processors are looking for work by themselves, we don't actively have to distribute work from the main thread (this has to be synced; if I understand correctly then via compare-and-swap).

Life of a spark

1. Creation of thunk/spark & push to queue
   • If already evaluated (called a dud) nothing happens, we just return the value.
   • If we have an overflow in the queue the spark is evaluated later (but not in parallel! this means we should take care to not create an unreasonable amount of sparks)
2. Upon successful spark creation with still have multiple options:
   • fizzled: already had to be evaluated (i.e. was stolen and evaluated first by another thread)
   • garbage collected: was not needed
   • converted: evaluated, yay.

The Eval Monad

To populate the spark queues of our system we will use a new type called Eval. Parallel computations themselves are represented by functions a -> Eval a. They represent the valuation of a value of type a with a certain strategy (which is why we also have a type called Strategy):

type Strategty a = a -> Eval a

The three most important and basic functions to work with Eval and Strategy are:

• rseq :: a -> Eval a evaluates to weak head normal form (WHNF). This is basically seq.
• rpar :: a -> Eval a creates a spark.
• runEval :: Eval a -> a gets a value out of Eval.

All we need to do now is apply those functions to the thunks we want to evaluate in parallel. In order to work with non-trivial types we will have to compose/sequence Strategys, which will of course be done with the monad instance of Eval.

Eval monad

The Eval monad is a super simple monad instance, but it lets us compose parallel computations:

data Eval a = Done a

runEval :: Eval a -> a
runEval (Done x) = x

instance Monad Eval where
  return :: a -> Eval a
  return x = Done x

  -- the pattern match in (Done x) *forces* evaluation
  -- of the value that is passed to >>=
  (>>=) :: Eval a -> (a -> Eval a) -> Eval a
  (Done x) >>= f = f x

Parallel pairs

We have different options for parallel evaluation of an expensive function f on a pair. For example, we can implement a strategy that just creates two sparks and returns immediately:

parPair :: (a,b) -> (a,b)
parPair (x,y) = runEval $ do
  x' <- rpar (f x)
  y' <- rpar (f y)
  return (x',y')

The Eval monad is strict in the first argument of >>= and therefore eagerly evaluates rpar (f x), which creates a spark. If Eval was not strict nothing would happen at all apart from creation of normal, new thunks. The dashed line in the figure below indicates when the retrun in parPair happens.

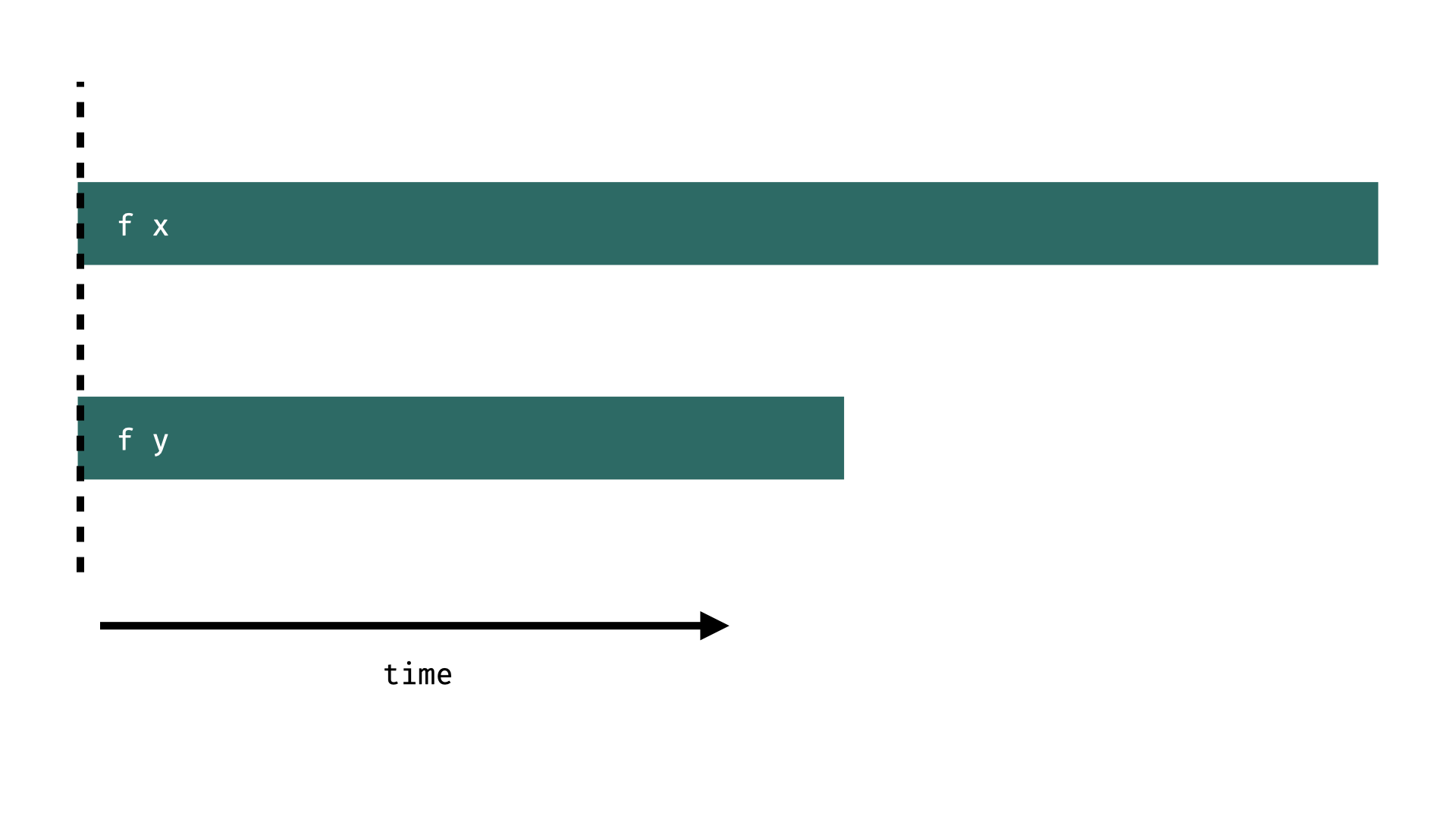
The examples here are taken from Simon Marlow's book, you can play with a scripts that nicely illustrates what is happening in rpar.hs.

Another strategy could be to return after f y is done by using rseq to evaluate f y to WHNF.

rseq

parSeqPair :: (a,b) -> (a,b)
parSeqPair (x,y) = runEval $ do
  x' <- rpar (f x)
  y' <- rseq (f y) -- wait until y' is done
  return (x',y')

rseq in separate line

parSeqPair :: (a,b) -> (a,b)
parSeqPair (x,y) = runEval $ do
  x' <- rpar (f x)
  y' <- rpar (f y) -- could be executed on another processor
  rseq y'          -- but we wait for it here
  return (x',y')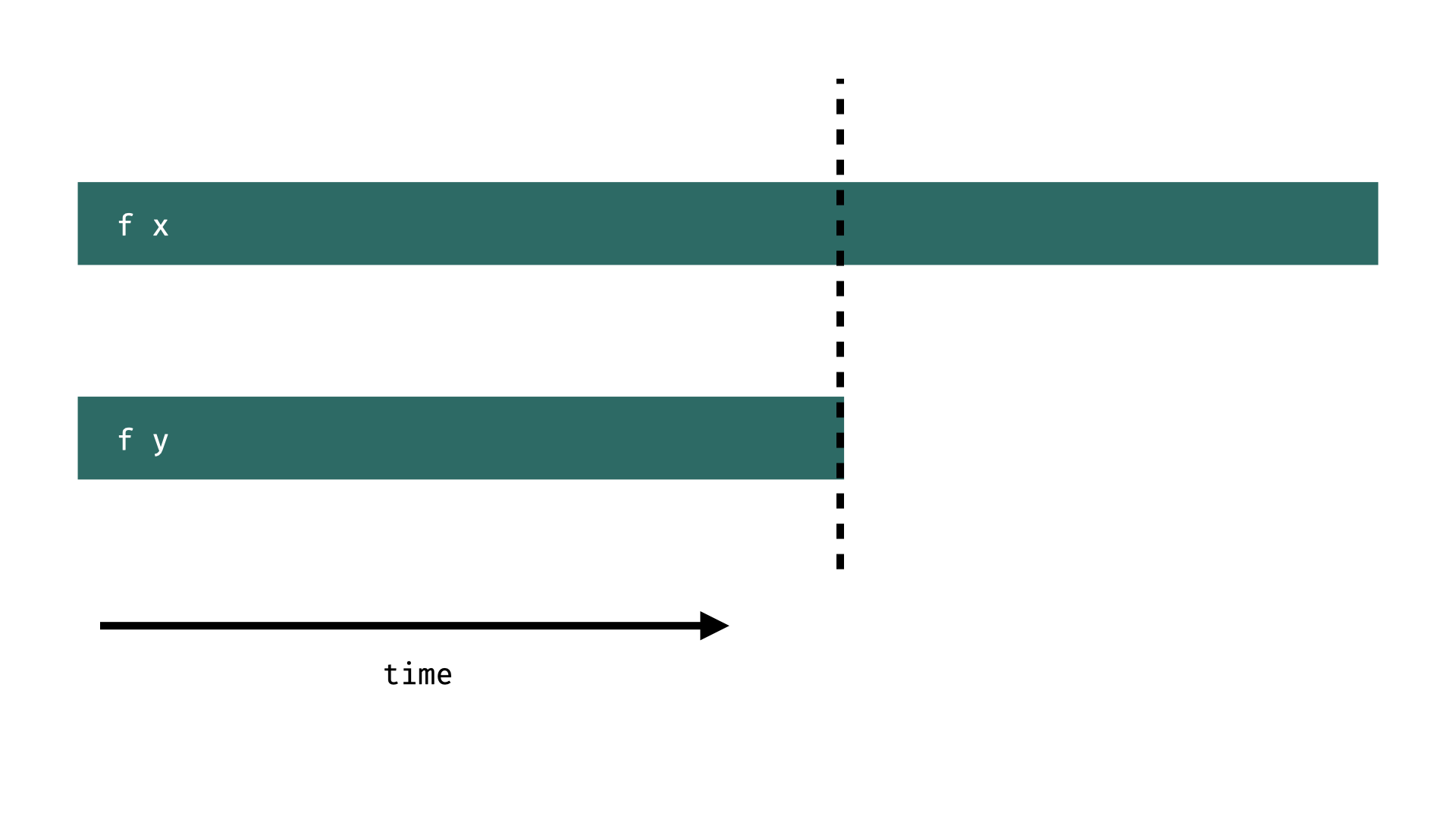

Parallel lists

With rpar / rseq we can implement a simple parallel map that evaluates every element of a list in parallel:

parMap :: (a -> b) -> [a] -> Eval [b]
parMap f [] = return []
parMap f (a:as) = do
  b  <- rpar  (f a)
  bs <- parMap f as
  return (b:bs)

With parMap we can solve a number of mazes with the solver from the labs. To run the file below you need the Parser.hs and Mazes.hs modules.

import System.Environment
import Control.Parallel.Strategies
import Data.Maybe

import Parser
import Mazes

main :: IO ()
main = do
  -- read maze files into strings
  fs <- getArgs
  ss <- mapM readFile fs

      -- parse mazes into [Maze]
  let ms = catMaybes (map (parse file) ss)
      -- solve them in parallel!
      xs = runEval $ parMap (solve . fst) ms

  -- make sure they are solved by checking if they are `Just`
  print $ length $ filter isJust xs

To actually run things in parallel you have to

# compile with rtsopts so that we can choose number of processors
ghc -threaded -rtsopts --make parmaze.hs

# run with one processor (-N1) and printed timings (-s)
./parmap +RTS -N1 -s -RTS maze1.txt maze2.txt ...
  Total   time    0.954s  (  0.976s elapsed)

# run with two processors (-N2) and printed timings (-s)
./parmap +RTS -N2 -s -RTS maze1.txt maze2.txt ...
  Total   time    1.003s  (  0.625s elapsed)

Evaluation strategies

The parMap function is nice and simple, but we can do slightly better by not implementing parallel versions of all higher order functions like filter or fold, but instead defining strategies for datatypes. These strategies will all return Strategy a = a -> Eval a, which will make them composable (and thus more general). This is possible, again, because Haskell is lazy. An unevaluated thunk of a list could be passed to different list strategies (e.g. something that creates a new spark for every element in the list like parMap or another strategy that divides the list into chunks before sparking). This is where Strategys become handy:

type Strategy a = a -> Eval a

using :: a -> Strategy a -> a
x `using` strat = runEval (strat x)

We can implement a parPair strategy

parPair strategy

parPair :: Strategy (a,b)
parPair (a,b) = do
  a' <- rpar a
  b' <- rpar b
  return (a',b')

-- annotate any pair with strategy
(f x, f y) `using` parPair

compare to old version

parPair :: (a,b) -> (a,b)
parPair (x,y) = runEval $ do
  x' <- rpar (f x)
  y' <- rpar (f y)
  return (x',y')

Finally, we can parametrize strategies to get the different pair evaluation strategies in one definition:

evalPair :: Strategy a -> Strategy b -> (a,b) -> Eval (a,b)
evalPair sa sb (a,b) = do
  a' <- sa a
  b' <- sb b
  return (a', b')

-- and now e.g. the second strategy
-- that returns after (f y) is done
(f x, f y) `using` evalPair rpar rseq

We can implement a parallel parList strategy with a common strategy for every individual element of the list:

parList :: Strategy a -> Strategy [a]
parList strat []     = return []
parList strat (x:xs) = do
  x'  <- rpar (x `using` strat)
  xs' <- parList xs strat
  return (x':xs')

This lets us define parMap like below:

parMap :: (a -> b) -> [a] -> [b]
parMap f xs = map f xs `using` parList rseq

where we use parList rseq to define a strategy that returns after the last element of the list is done evaluating.

Parallel Integrals

As a last example we can return to our integral example. A simple, sequential implementation is given in the example below. Instead of naively parallelizing this example with parListChunk we can also perform the accumulation step in the fold in chunks. This will introduces some overhead in the but when throwing enough compute at it we get a decent speedup. The updated lines are highlighted below.

Sequential

integral :: (Ord a, Floating a, Enum a) => (a -> a) -> a -> a -> a -> a
integral f step start end = sum quads
 where
  quad (a,b) = (b-a) * f ((a+b)/2)
  quads = map quad (zip (init steps) (tail steps))
  steps = [start, start+step .. end]

Parallel

integralchunk :: (Ord a, Floating a, Enum a) => (a -> a) -> a -> a -> a -> Int -> a
integralchunk f step start end chunksize = sum cs
 where
  cs = [sum xs | xs <- chunks chunksize quads] `using` parList rseq
  quad (a,b) = (b-a) * f ((a+b)/2)
  quads = map quad (zip (init steps) (tail steps))
  steps = [start, start+step .. end]

This example is stolen from here.

You can find a full script that compares the two approaches in pfold.hs.

# compile it
$ ghc -threaded -rtsopts --make pfold.hs

# run the sequential version
$ ./pfold 1
0.720329759982676
time: 2.6484s

# run the parallel version
$ ./pfold 2 +RTS -N8
0.72032975998268
time: 0.8188s

References

• parMap / parList derived
• Control.Parallel.Strategies
• Folds and parallelism among others explains foldl'