Lab 11: Functors and IO

Exercise 1

This is a warm-up exercise. Write a function converting a string into a CamelCase format. It takes a string, splits particular words separated by whitespace characters, changes the first letter of each word to uppercase, and joins all the words into a single string. E.g. " no air" is converted into "NoAir". Moreover, make the function polymorphic so that it works over any functor instance over String, i.e., our function should have the following type:

toCamelCaseF :: Functor f => f String -> f String

Solution

First, we need a function converting an alphabetic character into uppercase. In the library Data.Char there is a function toUpper doing that. We will implement this function ourselves. To represent the relation between lowercase and uppercase letters, we take a list of tuples [('a','A'), ('b','B'),...]. This can be created by zipping ['a'..'z'] and ['A'..'Z']. For a character c if it is a lowercase letter, then we return the corresponding uppercase letter; otherwise we return just c. To do that we can use the function

lookup :: Eq a => a -> [(a, b)] -> Maybe b

that takes an element of type a and a list of pairs and lookups the element among first components of those pairs. If it is there, it returns Just the second component and otherwise Nothing. Using the case expression, we can distinguish both cases by pattern matching.

Solution: toUpper

toUpper :: Char -> Char
toUpper c = case lookup c $ zip ['a'..'z'] ['A'..'Z'] of
    Nothing -> c
    Just c' -> c'

To split the input string into particular words, we can apply the function

words :: String -> [String]

Then we have to apply toUpper to the first letter of each word. Finally, concatenate the resulting words. Thus we have a function converting a string into a CamelCase string.

Solution: toCamelCase

toCamelCase :: String -> String
toCamelCase = concat . map toUpperHead . words where
    toUpperHead "" = ""
    toUpperHead (x:xs) = toUpper x:xs

It remains to lift the above function by fmap so that we can apply toCamelCase over any functor instance.

Solution: toCamelCaseF

toCamelCaseF :: Functor f => f String -> f String
toCamelCaseF = fmap toCamelCase

Examples:

> toCamelCaseF [" no air ", " get back"]  -- over the list functor
["NoAir","GetBack"]

> toCamelCaseF (Just " no air ")  -- over the Maybe functor
Just "NoAir"

> toCamelCaseF getLine   -- over IO functor
 no  air                 -- user's input
"NoAir"

Exercise 2

A deterministic finite automaton (DFA) is a tuple , where is a set of states, is a finite alphabet, is a transition function, is an initial state and is a set of final states. DFAs play a crucial role in applications of regular expressions as each regular expression can be converted into an equivalent DFA accepting the language defined by the regular expression. For instance, the regular expression [0-9]+\.[0-9][0-9] defines a language of numbers having the decimal point followed by two digits, e.g. , , . The equivalent automaton is depicted below. It has states Before, Digit, Dot, First, Second. Before is the initial state and Second is the only final state. Automaton reads the input characters and changes its state according to . After the whole input is read, it accepts the input string iff it is in a final state. At the beginning, it is in Before. Once it reads a digit, the state changes to Digit and remains there until . is read. Then the next digit changes the state to First and finally the second digit after the decimal point changes the state to Second which is final. Anything else leads to the state Fail.

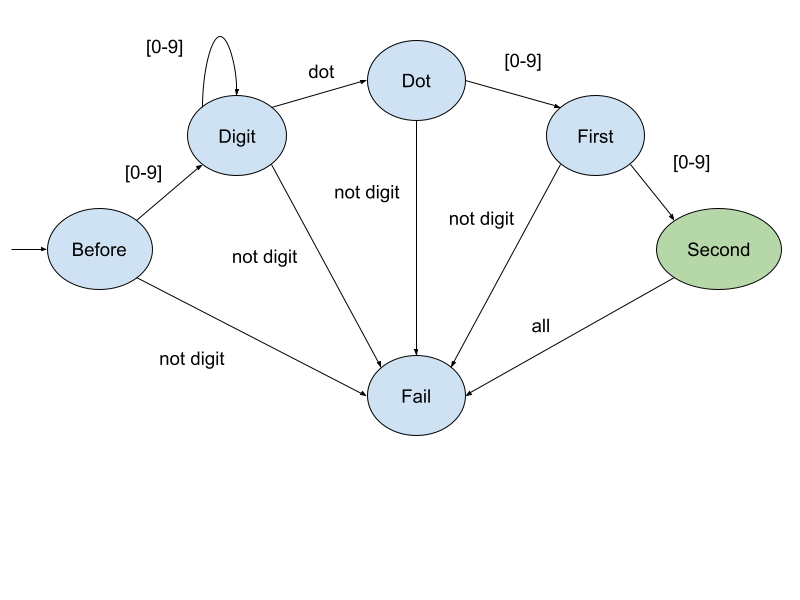
Our task is to define a parametric data type DFA a modelling a DFA and implement the function

evalDFA :: DFA a -> String -> Bool

taking an automaton, a string w and returning true if w is accepted by the automaton and false otherwise.

Further, define the above automaton and use it to implement a function

parseNum :: String -> Maybe Float

taking a string and returning Just the parsed floating number if the string is accepted by the automaton or Nothing. Finally, lift parseNum to any functor instance

parseNumF :: Functor f => f String -> f (Maybe Float)

Solution

To model an automaton, we need the transition function , the initial and final states. We make the type DFA a parametric over a type a representing states as we wish to work with automata whose states might be integers or strings or other data types. We could also make DFA a parametric over a type b representing the alphabet but for this example we set Char. Thus the transition function is of type a -> Char -> a. The initial state is of type a and the set of final states can be represented as a predicate of type a -> Bool.

data DFA a = Automaton (a->Char->a) a (a->Bool)

Now we can write the function simulating the automaton computation. It starts with the initial states and repeatedly applies the transition function to the current state and the current letter. This can be done by folding as I explained in the lecture introducing folding in Scheme. In the comment below, you can see how to implement the automaton computation directly without folding. Finally, the predicate defining the final states is applied.

Solution: evalDFA

evalDFA :: DFA a -> String -> Bool
evalDFA (Automaton dlt s inF) w =
    inF (foldl dlt s w)
--  inF (deltaStar s w)
--  where deltaStar q [] = q
--       deltaStar q (a:ws) = deltaStar (dlt q a) ws

Now we represent the above automaton as an instance of DFA a. We first define a type representing the states. Then we define the automaton over these states.

data State = Before | Digit | Dot | First | Second | Fail

isNum :: Char -> Bool
isNum c = c `elem` ['0'..'9']

final :: State -> Bool
final Second = True
final _ = False

delta :: State -> Char -> State
delta Before c | isNum c = Digit
               | otherwise = Fail
delta Digit c | isNum c = Digit
              | c == '.' = Dot
              | otherwise = Fail
delta Dot c | isNum c = First
            | otherwise = Fail
delta First c | isNum c = Second
              | otherwise = Fail
delta Second _ = Fail
delta Fail _ = Fail

automaton :: DFA State
automaton = Automaton delta Before final

Next, the function parseNum takes a string, and uses the automaton to check if the string has the correct format. If yes, it is read by the read function and otherwise Nothing is returned.

Solution: parseNum

parseNum :: String -> Maybe Float
parseNum w = if evalDFA automaton w then Just (read w)
             else Nothing

Now, we can lift it via fmap.

Solution: parseNumF

parseNumF :: Functor f => f String -> f (Maybe Float)
parseNumF = fmap parseNum

Examples:

> parseNumF ["234", "123.12", ".5", "0.50"]  -- the list functor instance
[Nothing,Just 123.12,Nothing,Just 0.5]

> parseNumF getLine   -- IO functor instance
1234.34               -- user's input
Just 1234.34

> parseNumF getLine   -- IO functor instance
1.234                 -- user's input
Nothing

Exercise 3

Using the function parseNumF from the previous exercise, write a function parseIO :: IO () that displays a string "Enter number:\n" and then reads from the keyboard a string. If the string has the correct format (i.e., number with two digits after the decimal point), then it displays "Ok"; otherwise it asks for the user's input again.

Solution

First, we execute the action putStrLn displaying the string "Enter number:". Then we execute the action parseNumF getLine :: IO (Maybe Float). Depending of its result, we either display "Ok" or execute the whole action parseIO again. We can either use the monadic operators as follows:

Solution: using bind

parseIO :: IO ()
parseIO = putStrLn "Enter number:"
          >> parseNumF getLine
          >>= \x -> case x of
                      Nothing -> parseIO
                      Just _ -> putStrLn "Ok"

or we can use the do-syntax as follows:

Solution: using do

parseIO :: IO ()
parseIO = do putStrLn "Enter number:"
             x <- parseNumF getLine
             case x of
               Nothing -> parseIO
               Just _ -> putStrLn "Ok"

Task 1

Consider the following data type representing Boolean propositional formulas built up from atoms by negations, conjunctions, and disjunctions.

data Expr a = Atom a
            | Neg (Expr a)
            | And (Expr a) (Expr a)
            | Or (Expr a) (Expr a)
                deriving (Eq, Show)

The type constructor Expr has a single parameter a representing a data type for atoms. So for instance Expr Bool is a Boolean expression that can be directly evaluated, e.g. the expression is represented as

expr :: Expr Bool
expr = Or (And (Atom True) (Neg (Atom False))) (Atom False)

On the other hand, Expr String might represent propositional formulas whose atoms are variables represented as strings, e.g. the formula is represented as

fle :: Expr String
fle = And (Or (Neg (Atom "x")) (Atom "x")) (Atom "y")

Write a function eval :: Expr Bool -> Bool evaluating a given Boolean expression. Thus it should evaluate expr to True. Further, implement a function getAtoms :: Expr a -> [a] returning the list of atoms for a given expression, e.g. getAtoms fle should return ["x","x","y"].

Hint

Logical operations negation, conjunction and disjunction can be respectively computed by not, &&, ||. The last two are infix operators.

Solution: eval

eval :: Expr Bool -> Bool
eval (Atom c) = c
eval (Neg e) = not (eval e)
eval (And e1 e2) = eval e1 && eval e2
eval (Or e1 e2) = eval e1 || eval e2

Solution: getAtoms

getAtoms :: Expr a -> [a]
getAtoms (Atom c) = [c]
getAtoms (Neg e) = getAtoms e
getAtoms (And e1 e2) = getAtoms e1 ++ getAtoms e2
getAtoms (Or e1 e2) = getAtoms e1 ++ getAtoms e2

Task 2

The type constructor Expr from the previous task can be made into an instance of Functor as follows:

instance Functor Expr where
    fmap f (Atom c) = Atom (f c)
    fmap f (Neg e) = Neg (fmap f e)
    fmap f (And e1 e2) = And (fmap f e1) (fmap f e2)
    fmap f (Or e1 e2) = Or (fmap f e1) (fmap f e2)

Thus if we have a map f :: a -> b, it can be lifted by fmap to a map of type Expr a -> Expr b. This might be handy if we need to rename variables or we want to assign concrete Boolean values to variables. Write a polymorphic function

subst :: Functor f => [String] -> f String -> f Bool

taking a list of strings (variables) and a data structure over strings returning the same data structure where the strings (variables) in the input list are replaced by True and the rest by False. Use the lifting by fmap.

Solution: subst

subst :: Functor f => [String] -> f String -> f Bool
subst xs = fmap (`elem` xs)

Next, apply the function subseqs :: [a] -> [[a]] from the previous lab returning a list of all sublists of a given list.

subseqs :: [a] -> [[a]]
subseqs [] = [[]]
subseqs (x:xs) = subseqs xs ++ [x:ys | ys <- subseqs xs]

The above function can generate all possible evaluations of a propositional formula if we apply it to the result of getAtoms. Implement functions

isTaut, isSat :: Expr String -> Bool

testing whether a given formula is a tautology (resp. satisfiable). A propositional formula is satisfiable if there exists an evaluation of atoms such that the Boolean expression resulting from the replacing atoms by the respective Boolean values is evaluated to True. A propositional formula is called tautology if it is satisfied by all possible evaluations of its atoms.

Hint

To check that there exists an evaluation satisfying a formula or if all evaluations satisfy the formula, use the functions or, and respectively. These functions are applicable to any list of Boolean values.

Solution: isTaut, isSat

check :: ([Bool] -> Bool) -> Expr String -> Bool
check g e = g [ eval $ subst vs e | vs <- vss]
    where vss = subseqs $ getAtoms e

isTaut, isSat :: Expr String -> Bool
isTaut = check and
isSat = check or