Macros & Interpreters

Syntactic macros

The following section should only briefly introduce syntactic macros. At the same time, I will explain a related topic on how Racket processes source files. What happens if we press the Run button in DrRacket or execute racket source.rkt in a shell?

1. Racket must first parse our source file consisting of a sequence of characters. In other words, the sequence of characters is converted into a data structure. This data structure is called Abstract Syntax Tree (AST) and contains all the information extracted from the source file, i.e., our expressions, definitions, etc. Due to the homoiconicity of Racket, Racket's syntax directly corresponds to regular lists. Thus AST is represented through lists. For example, if our source file contains (+ (* 2 3) 4), AST is a list whose first element is +, followed by a list (* 2 3), and 4. Moreover, each part of AST is enriched by further syntactic information, e.g., the corresponding line and column in the source file.

2. Once AST is created, Racket executes various transformations on AST. In fact, some Racket syntactic constructions are implemented as transformations on AST. For example, the expression (and exp1 exp2 exp3) is transformed into

(if exp1
    (if exp2
        exp3
        #f)
    #f)

3. When AST consists only of basic syntactic constructions, a compiler translates AST into a machine code that can be executed.

The workflow is depicted below:

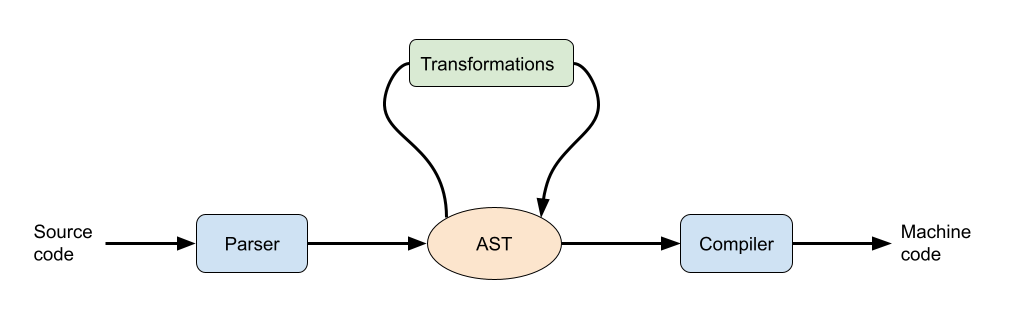
If we create a Racket program, its expressions get evaluated in the runtime, i.e., after the compilation phase. On the other hand, syntactic macros allow us to add some extra transformations into the second phase before the compilation. Macros are basically functions operating on AST. Thanks to the homoiconicity, AST is represented as usual data in Racket. Thus macros can be defined as usual Racket functions.

Implementing macros is a complex topic. The simplest way to introduce a macro is based on pattern matching. We specify a syntax rule consisting of a pattern and a template on how the pattern should be rewritten. Racket tries to match the pattern against pieces of our code. Once there is a match, the corresponding portion of the code is rewritten according to the template.

Recall the function my-if, whose parameters must be passed as thunks. We cannot eliminate those thunks because the parameters get evaluated before the function body. However, injecting them before the compilation by a macro is possible.

(define-syntax-rule (macro-if c a b)
  (my-if c (thunk a) (thunk b)))

(define (my-if c a b)
  (if c (a) (b)))

The macro defines a syntax rule whose pattern is (macro-if c a b). Racket searches for a portion of AST being a list of length starting with a symbol macro-if. If such a list is found, it is rewritten into (my-if c (thunk a) (thunk b)). Thus we can use in our code macro-if instead of my-if. Racket automatically translates all occurrences of macro-if to my-if with the thunks injected.

A macro can be composed of several syntax rules. We can specify several patterns to be matched against the AST and templates for each pattern. If any pattern matches, the corresponding template defines how to rewrite the code. For example, let us implement a macro introducing comprehension terms into Racket. A comprehension term allows us to define a new list from a list by means of an expression and predicate. They are common in Python. For instance,

python> [x**2 for x in range(5)]
[0, 1, 4, 9, 16]

python> [x for x in range(20) if x % 2 == 0]
[0, 2, 4, 6, 8, 10, 12, 14, 16, 18]

We want to define a similar syntax for Racket via a macro. We will express the above Python examples in Racket as follows:

> (list-comp (* x x) : x <- (range 5))
'(0 1 4 9 16)

> (list-comp x : x <- (range 20) if (even? x))
'(0 2 4 6 8 10 12 14 16 18)

We must define a macro with two syntax rules to make the new syntax work—one for the comprehension term without and one for the comprehension term with an if clause.

(define-syntax list-comp
  (syntax-rules (: <- if)
    [(list-comp <expr> : <id> <- <lst>)
     (map (lambda (<id>) <expr>) <lst>)]

    [(list-comp <expr> : <id> <- <lst> if <cond>)
     (map (lambda (<id>) <expr>)
          (filter (lambda (<id>) <cond>) <lst>))]))

Line 3 defines a pattern for the comprehension term without an if clause. Line 4 specifies how to rewrite the comprehension term. The symbol <id> together with the expression <exp> define a function to be applied to each element of the list <lst>. Line 6 represents the second pattern containing the if clause. In that case, we must first filter the list <lst> based on the if clause (Line 8) and then apply the function to each element of the filtered list (Line 7).

More on Macros

If you want to read more about Macros, good starting points are the Beautiful Racket explainers on macros, hygiene, syntax patterns, and of course the Racket docs.

Interpreters

Interpreters are programs that directly^[1] execute instructions of a programming language (in our case that means evaluating S-expressions). Before we can create an interpreter for a given programming language we need to define the language itself. Generally, programming languages are composed of two parts:

• Syntax: Tells you what kind of expressions you can write to obtain a valid program. The grammar defines how larger expression are built from primitives.
• Semantics: Assigns meaning of certain primitives. For example, it can define what the operation + does.

Based on a well defined language interpreters usually work in two major phases. After you provide the source code, the interpreter first parses^[2] the text into an abstract syntax tree (AST). Then the AST is evaluated to produce the final output.

In the case of LISP-like languages we already wrote our code in terms of S-expressions, which means that we don't have to worry about parsing our code at all! Parsing is provided for free by the racket language, because it is homoiconic^[3]. Meaning, our source code is already written as a nested list. Hence, we will only have to worry about the evaluation of given S-expressions.^[4]

Brainf*ck

Interpreting a full-fledged programming language is quite tricky, so we will choose a very simple language to interpret, called Brainf*ck. Here is an example of a valid Brainf*ck program (we will see what it does in a little while):

,>,[-<+>]<.

Most of the characters above represent operations on a tape of numbers (which typically is filled with zeros at the start of the program) and a pointer to the current position on the tape:

  ↓
0 0 0 0 0 0 0 ...
  ↑

The different operations can e.g. increment the number at the current pointer position, or move the pointer. The full list of operations can be found in the table below. In addition to the tape, the user can also provide data to a program via a list of inputs.

Character	Meaning
>	Increment the data pointer by one (to point to the next cell to the right).
<	Decrement the data pointer by one (to point to the next cell to the left).
+	Increment the byte at the data pointer by one.
-	Decrement the byte at the data pointer by one.
.	Output the byte at the data pointer.
,	Accept one byte of input, storing its value in the byte at the data pointer.
[ code ]	While the number at the data pointer is not zero, execute code.

With the table above we can decipher the first example program ,>,[-<+>]<.: Let's assume we have two numbers waiting in our input list and a fresh tape:

input: '(2 3)
tape:
↓
0 0 0 0 0 0 0 ...
↑

1. ,: Read a number from the input and store it at the pointer position. Now input and tape look like this:

input: '(3)
tape:
↓
2 0 0 0 0 0 0 ...
↑

2. >: Move pointer to right.
3. ,: Read a second number from the input. Now the input is empty and the tape contains the two number we read:

input: '()
tape:
  ↓
2 3 0 0 0 0 0 ...
  ↑

4. [-<+>]: Is a cycle, which we will keep executing until the number at the current pointer is zero. Currently, it is 3, so we run the cycle. The cycle itself contains four operations which decrement the number at the current position, move the pointer to the left, increment the number there, and finally moves the pointer back to the right.

input: '()
tape:
  ↓
3 2 0 0 0 0 0 ...
  ↑

5. The cycle is repeated another two times until the current pointer is zero:

input: '()
tape:
  ↓
5 0 0 0 0 0 0 ...
  ↑

6. <.: Finally, we move the pointer to the left again, and output the current value.

We just added two numbers!

---

More formally, Brainf*ck is a minimalistic, esoteric programming language that defines computations over a fixed-size tape of numbers. The syntax grammar of the language is given by

<program> -> <term>*
<term>    -> <cmd> | <cycle>
<cycle>   -> [<program>]
<cmd>     -> + | - | < | > | . | ,

which means that a <program> is a sequence of <term>s. Each term is either a command (<cmd>) or a <cycle>. We already listed the six possible commands above. Inside cycles we can nest whole programs which gives us the ability to write arbitrary loops. Thus, we can write a syntactically well-formed expression simply with arbitrary sequence of commands. The only thing we have to take care of is to match parentheses appropriately.

For our interpreter, we will represent Brainf*ck programs simply as lists of terms. Cycles will form nested lists. To make things more convenient for us we will slightly alter the syntax of Brainf*ck, because . and , are already taken in Racket (for pairs and quoting). We will substitute them by @ and *, respectively:

Character	Substitue	Meaning
>	>	Increment the data pointer by one (to point to the next cell to the right).
<	<	Decrement the data pointer by one (to point to the next cell to the left).
+	+	Increment the byte at the data pointer by one.
-	-	Decrement the byte at the data pointer by one.
.	@	Output the byte at the data pointer.
,	*	Accept one byte of input, storing its value in the byte at the data pointer.
[ code ]	[code]	While the number at the data pointer is not zero, execute code.

With the substitutions we can define our addition program as

(define add-prg '(@ > @ [- < + >] < *))

Our final implementation will define a function run-prg which accepts a program and some input, for example:

> (run-prg add-prg '(12 34))
46

Mutable Tape

During the lecture we will use a global, mutable tape (bad!) to implement our interpreter (you will modify this implementation to use an immutable tape during the labs).

Vectors: make-vector, vector-ref, and vector-set!.

We are not discussing mutable data-structures in this course, but Racket does support them. Here we only briefly show you Vectors so that you can get rid of them again during the labs. Racket's vectors are fixed-length arrays with constant-time access and update of their elements numbered from 0.

For the purposes of this initial interpreter implementation we only need the following functions:

> (define v (vector 1 2 3))
> v
'#(1 2 3)

> (vector-ref v 2)
3

> (vector-set! v 2 "hi")
> v
'#(1 2 "hi")

> (make-vector 4 'a)
'#(a a a a)

Our tape will be represented by a mutable vector of numbers which we can initialize with

> (define SIZE 10)
> (define t (make-tape SIZE 0))
'#(0 0 0 0 0 0 0 0 0 0)

And mutate via the vector-set! function.

> (vector-set! t 2 5)
> t
'#(0 0 5 0 0 0 0 0 0 0)

We will implement the tape and the possible operations on the tape by defining a closure. The closure will hold the tape itself, a pointer ptr to the current position, and will accept a number of messages msg that trigger operations on the tape:

(define (make-tape size)
  (define tape (make-vector size 0))
  (define ptr 0)

  (lambda (msg)
    (cond
      [(eqv? msg 'tape) (list tape ptr)]
      [(eqv? msg 'plus) (vector-set! tape ptr (+ 1 (vector-ref tape ptr)))])))

The tape can then be used like this:

> (define tp (make-tape SIZE))
> (tp 'tape) ; output tape and pointer
'(#(0 0 0 0 0 0 0 0 0 0) 0)

> (tp 'plus)

> (tp 'tape)
'(#(1 0 0 0 0 0 0 0 0 0) 0)

Command Implementation

Implementing the operations for the commands <, >, +, -, @, and . is now straightforward:

(define (make-tape size)
  (define tape (make-vector size 0))   ; initialize fresh tape
  (define ptr 0)                       ; pointer points to the first element

  (define (change op ptr)
    (vector-set! tape ptr (op (vector-ref tape ptr) 1)))

  (define (move op ptr)
    (let ([new-ptr (op ptr 1)])
      (if (or (< new-ptr 0) (> new-ptr size))
          (error "Moving outside tape")
          new-ptr)))

  (lambda (msg)
    (match msg
      ['tape (list tape ptr)]
      ['plus (change + ptr)]
      ['minus (change - ptr)]
      ['left (set! ptr (move - ptr))]
      ['right (set! ptr (move + ptr))]
      ['dot (vector-ref tape ptr)]
      ['comma (lambda (val) (vector-set! tape ptr val))]
      ['reset (vector-fill! tape 0) (set! ptr 0)])))

Wit the code above we can already manually run instructions on our tape that resemble Brainf*ck programs:

> (define t (make-tape SIZE))
> (t 'tape)
'(#(0 0 0 0 0 0 0 0 0 0) 0)

> ((t 'comma) 2)  ; read the number 2 from an input
> (t 'tape)
'(#(2 0 0 0 0 0 0 0 0 0) 0)

> (t 'right)
> ((t 'comma) 3) ; read the number 3 from an input
> (t 'tape)
'(#(2 3 0 0 0 0 0 0 0 0) 1)

Program evaluation

In order to evaluate whole Brainf*ck programs we now just have to implement a function that accepts a program (as a nested list of operations) and a list of inputs. The user-facing function of our interpreter, run-prg will look very simple:

(define (run-prg prg input)
  (tape 'reset)              ; fill tape by zeros
  (eval-prg prg input)       ; evaluate program
  (displayln "done"))

With pattern matching the eval-prg function can conveniently be split into four cases:

1. If we end up with an empty prg we are at the end of our program and simply output the current input.
2. When encountering an '@-symbol we want to read from the input. This is the only time we directly work with the input list, so this case deserves its own function.
3. If the current element in the prg list is again a list, we execute a separate cycle function.
4. Otherwise we call our tape operations according to the current symbol.

(define (eval-prg prg input)
  (log prg input)
  (match prg
    [(list) input]  ; are all commands processed? if yes, return remaining input
    [(list '@ rest ...) (eval-comma rest input)]
    [(list (? list? cycle) rest ...) (eval-cycle cycle rest input)]
    [(list cmd rest ...) (eval-cmd cmd rest input)]))

The last case where we just need to translate symbols to tape operations is the simplest to implement:

(define (eval-cmd cmd prg input)
  (match cmd
    ['+ (tape 'plus)]
    ['- (tape 'minus)]
    ['< (tape 'left)]
    ['> (tape 'right)]
    ['* (printf "~a " (tape 'dot))]
    [_ (error "Unknown command")])
  (eval-prg prg input))   ; recursive call processing further commands

Note that we are mutating the global tape in the match clause and then do a mutually recursive call to eval-prg to continue processing the rest of the program.

If we want to read from an input, we strip on element off the input, store it on the tape, and again continue the evaluation of the rest of prg.

(define (eval-comma prg input)
  (cond
    [(null? input) (error "Empty input")]
    [else ((tape 'comma) (car input))
          (eval-prg prg (cdr input))]))  ; recursive call processing further commands

To run a cycle, we check that the current value is not zero, evaluate the cycle, and then call eval-cycle again (with potentially changed input list). If the current value is zero at the beginning of the cycle, we skip its evaluation.

(define (eval-cycle cycle prg input)
  (if (= (tape 'dot) 0)                         ; is cycle is finished?
      (eval-prg prg input)                      ; if yes, recursive call preocessing further commands
      (let ([new-input (eval-prg cycle input)]) ; otherwise evaluate cycle code
        (eval-cycle cycle prg new-input))))     ; and execute the cycle again

We are done! The complete implementation of our interpreter can be found here. Running our interpreter on the add-prg will produce the following output:

> (run-prg add-prg '(2 3))
tape: (#(0 0 0 0 0 0 0 0 0 0) 0)  input: (2 3)  cmd: @
tape: (#(2 0 0 0 0 0 0 0 0 0) 0)  input:   (3)  cmd: >
tape: (#(2 0 0 0 0 0 0 0 0 0) 1)  input:   (3)  cmd: @
tape: (#(2 3 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: (- < + >)
tape: (#(2 3 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: -
tape: (#(2 2 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: <
tape: (#(2 2 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: +
tape: (#(3 2 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: >
tape: (#(3 2 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd:
tape: (#(3 2 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: -
tape: (#(3 1 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: <
tape: (#(3 1 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: +
tape: (#(4 1 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: >
tape: (#(4 1 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd:
tape: (#(4 1 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: -
tape: (#(4 0 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: <
tape: (#(4 0 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: +
tape: (#(5 0 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: >
tape: (#(5 0 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd:
tape: (#(5 0 0 0 0 0 0 0 0 0) 1)  input:    ()  cmd: <
tape: (#(5 0 0 0 0 0 0 0 0 0) 0)  input:    ()  cmd: *
5

For larger programs you can take a look at some more examples or, of course, write your own Brainf*ck programs!

---

1. Interpreters directly execute programs, while compilers translate one language into another (typically a from a higher-level to a lower level language). ↩︎

2. Parsing can include an initial lexing phase which generates tokens from your code without creating a tree structure, and only then outputting an AST. ↩︎

3. Homoiconicity essentially means code == data, so that programs that are written in homoiconic languages can immediately be used as data-structures (in our case: lists). ↩︎

4. If you have been looking forward to a lecture on parsing and are now disappointed, do not despair, we will have a full lecture on monadic parsing in a few weeks during the Haskell part of this course. ↩︎