Lab 4: Higher-order functions and tree recursion

Exercise 1

Write a function (permutations lst) taking a list lst and returning all its permutations. For example

> (permutations '(1 2 3))
'((1 2 3) (2 1 3) (2 3 1) (1 3 2) (3 1 2) (3 2 1))

Suppose that we have all permutations of a list of length , and we want to build all permutations of its extension by an element. To do that, it suffices to take the element and interleave it in all possible ways into all the permutations of length .

For instance, ((2 3) (3 2)) are all permutations of the list (2 3). If we want to compute all permutations of (1 2 3), we take each permutation of length 2 and interleave the element 1 into it as follows:

(2 3) => ((1 2 3) (2 1 3) (2 3 1))
(3 2) => ((1 3 2) (3 1 2) (3 2 1))

Appending all these lists gives us the desired permutations of (1 2 3).

Write first a function interleave taking an element, a list, and returning all possible ways of inserting the element into the list. Using this function, devise the function permutations using the recursion on the length of lst.

Solution

(define (interleave el lst)
  (if (null? lst)
      ; there is only a single way one can insert el into '()
      (list (list el))
      ; otherwise one possibility is to prepend el to lst
      (cons (cons el lst)
            ; for the rest take all possible insertions of el into (cdr lst)
            (map (curry cons (car lst))
                 ; and prepend (car lst) to each of them
                 (interleave el (cdr lst))))))

(define (permutations lst)
  (if (null? lst)
      '(())
      (apply append
             ; into each permutation of (cdr lst) interleave (car last)
             (map (curry interleave (car lst)) (permutations (cdr lst))))))

Note

The permutations function is a great candidate for an application of streams. If you try to run (permutations (range 10)) you will run out of memory with the default DrRacket settings, while you can easily construct a stream of permutations with the (builtin) in-permutations function.

Exercise 2

Binary decision trees represent Boolean functions, i.e., functions from to . Let be a Boolean function. The corresponding binary decision tree is created as follows:

• Each input variable induces the th-level in the tree whose nodes are labelled by .
• Leaves are elements from .

Each path from the root to a leaf encodes an evaluation of input variables. If the path in an internal node goes to the left, the variable is evaluated by . If to the right, it is evaluated by . The leaf in the path represents the value for the evaluation defined by the path. Example of a Boolean function and its binary decision tree:

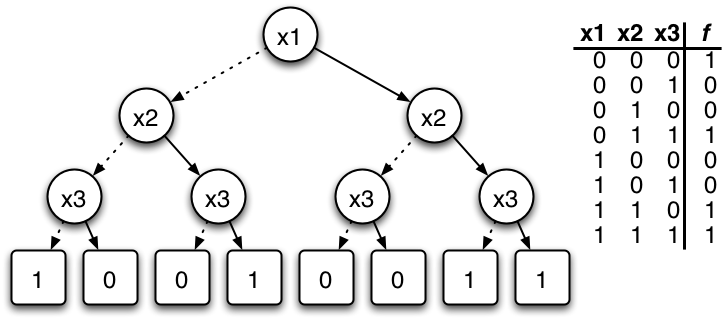
We will represent the inner variable nodes as Racket structures:

(struct node (var left right) #:transparent)

For instance, the above tree is represented as follows:

(define bool-tree
  (node 'x1
        (node 'x2
              (node 'x3 1 0)
              (node 'x3 0 1))
        (node 'x2
              (node 'x3 0 0)
              (node 'x3 1 1))))

Your task is to implement two functions. The first one (evaluate tree vals) takes a binary decision tree tree representing a Boolean function , a list vals of values of variables and returns . E.g.

(evaluate bool-tree '(1 0 1)) => 0
(evaluate bool-tree '(0 1 1)) => 1

The second function (satisficing-evaluations tree) takes a binary decision tree tree representing a Boolean function and returns all its satisficing evaluations, i.e., those for which . To represent a variable assignment, we introduce the following structure:

(struct assignment (var val) #:transparent)

An evaluation is a list of assignments for all variables occurring in the tree. Thus the output of satisficing-evaluations might look as follows:

(satisficing-evaluations bool-tree) =>
(list
 (list (assignment 'x1 0) (assignment 'x2 0) (assignment 'x3 0))
 (list (assignment 'x1 0) (assignment 'x2 1) (assignment 'x3 1))
 (list (assignment 'x1 1) (assignment 'x2 1) (assignment 'x3 0))
 (list (assignment 'x1 1) (assignment 'x2 1) (assignment 'x3 1)))

We devise two versions of evaluate. The first is the recursive function consuming consecutively values of and, based on its value, recursively evaluates either the left or right subtree. Once all the values are consumed, we should be in a leaf specifying the value of .

Soluiton: evaluate #1

(define (evaluate tree vals)
  (match vals
    [(list) tree]
    [(list 0 vs ...) (evaluate (node-left tree) vs)]
    [(list 1 vs ...) (evaluate (node-right tree) vs)]))

The second version uses higher-order functions. It converts the list of values of into the list of functions node-left, node-right corresponding to the path defined by vals. Finally, it applies their composition to tree.

Solution: evaluate #2

(define (evaluate2 tree vals)
  (define (left-right x)                         ; define function 0 -> node-left, 1 -> node-right
    (if (zero? x) node-left node-right))
  ((apply compose (map left-right (reverse vals))) tree))  ; map it over vals, compose the resulting functions and apply to tree

The function satisficing-evaluations is a recursive function using an accumulator ev, keeping partial evaluation as we traverse the tree. It recursively finds all satisficing evaluations of the left and right subtree, extends them by (resp. ) if they come from left (resp. right), and append them together.

Solution satisficing-evaluations

(define (satisficing-evaluations tree [ev '()])
  (match tree
    [1 (list (reverse ev))]        ; we reverse the evaluation so that the root variable comes first
    [0 '()]
    [(node v l r)
     (append (satisficing-evaluations l (cons (assignment v 0) ev))
             (satisficing-evaluations r (cons (assignment v 1) ev)))]))

Task 1

Write a function (sub-seq lst) taking a list lst and returning a list of all its sublists/subsequences. E.g.

(sub-seq '(1 2 3)) =>
  (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))

Hint

Code it as a recursive function using the following facts. 1) There is only a single subsequence of the empty list, namely the empty list. 2) Subsequences of are just subsequences of together with subsequences starting with and following by a subsequence of .

Solution

(define (sub-seq lst)
  (if (null? lst)
      '(())
      (let ([el (car lst)]
            [rest-sub-seq (sub-seq (cdr lst))])
        (append rest-sub-seq
                (map (curry cons el) rest-sub-seq)))))

Task 2

Consider a binary tree representing a tournament. Each internal node corresponds to a match. We represent it as the following structure:

(struct mtch (winner left right) #:transparent)

Leaves are of the form '<team>. E.g.

(define tour
  (mtch 'F
        (mtch 'D
              (mtch 'A 'A 'B)
              (mtch 'D 'C 'D))
        (mtch 'F
              (mtch 'F 'E 'F)
              (mtch 'G 'G 'H))))

represents the following tree:

                 F
                / \
               /   \
              /     \
             /       \
            /         \
           D           F
          / \         / \
         /   \       /   \
        A     D     F     G
       / \   / \   / \   / \
      A   B C   D E   F G   H

Write a function (beaten-teams tree) taking a binary tournament tree and outputting the list of beaten teams by the winner. E.g., (beaten-teams tour) => (E G D).

Hint

Code it as a recursive function starting in the root defining the tournament winner. Then follow the path labelled by the winner and collects the beaten teams along the path to an accumulator. You can use nested patterns in pattern matching to find out the losers.

Solution

(define (beaten-teams tree [acc '()])
  (match tree
    [(mtch win win r) (cons r acc)]
    [(mtch win l win) (cons l acc)]
    [(mtch win (mtch win l r) (mtch los _ _)) (beaten-teams (mtch win l r) (cons los acc))]
    [(mtch win (mtch los _ _) (mtch win l r)) (beaten-teams (mtch win l r) (cons los acc))]))