Monoids & Foldables

The fold operation is one of (if not the) most important construction in functional programming. An example we have seen very often already is using foldr to sum a list of numbers:

𝝺> sum = foldr (+) 0
𝝺> sum [1,2,3]
6

But there are many more things we can do with a fold! Another example is to define and:

𝝺> and = foldr (&&) True
𝝺> and [True,True,True]
True

𝝺> and [True,False]
False

An perhaps a tiny bit more interesting, counting the number of a specific element in a list:

𝝺> count e = foldr (\x acc -> if e==x then acc+1 else acc) 0
𝝺> count 2 [1,2,1,2,2,3]
3

Arguably the most advanced example we have seen of a fold is the monadic fold of mazes in setPath of Lab 12.

Importantly, we can implement a number of useful functions in terms of fold, so theoretically, we don't need much more than a datastructure being foldable. For example:

length = foldr (\_ -> (+1)) 0
map f = foldr ((:) . f) []

Fold: Aggregation & traversal

If we take a look at the type signature of foldr we see that it contains a Foldable type constraint:

foldr :: Foldable t => (b -> a -> b) -> b -> t a -> b

In this lecture we will explore the essence of this Foldable typeclass and pick at the different parts that make a fold. Conceptually, there are two parts to folding:

1. The aggregation - represented by the function b -> a -> b. We will use an abstraction called a Monoid to treat this part of the fold separately.
2. The traversal - which walks over the foldable datastructure t a. This is what the Foldable typeclass is doing.

Semigroups

Before we get to monoids which represent the aggregation part of a fold, we will define a semigroup.

A semigroup is a $⟨S,\diamond ⟩$ is a set $S$ equipped with a binary operation $\diamond :S\times S\to S$ that satisfies the associative property

$$a\diamond (b\diamond c)=(a\diamond b)\diamond c.$$

For example, addition on the natural numbers forms a semigroup: The domain $\mathbb{N}$ with the operation $+$ satisfies associativity: $a+(b+c)=(a+b)+c$.

In Haskell, the typclass Semigroup defines an operation <> :: a -> a -> a.

class Semigroup a where
  (<>) :: a -> a -> a

For lists we can implement semigroup simply with ++:

instance Semigroup [a] where
  (<>) = (++)

> [1,2,3] <> [4,5,6]
[1,2,3,4,5,6]

Monoids

A monoid $⟨M,\diamond ,u⟩$ is a semigroup with a unit $u\in M$ that satisfies

$$u\diamond a=a=a\diamond u.$$

In other words, a monoid has an identity element (e.g. for $+$ this element would be $0$).

Some examples of monoids are:

• $⟨\mathbb{N},+,0⟩$ - Addition of natural numbers
• $⟨\mathbb{N},\times ,1⟩$ - Multiplication of natural numbers
• $⟨$ [a], ++ , [] $⟩$ - Lists and concatenation
• $⟨A^A,\circ ,\text{id}⟩$ - Selfmaps $f:A\to A$ form a monoid under composition $\circ$.

The Monoid typeclass adds the identity element mempty

class Semigroup a => Monoid a where
  mempty :: a

which for the list monoid is the empty list.

instance Monoid [a] where
  mempty = []

For Ints we already noticed that we can have multiple monoids. To define a monoid over addition we therefore need a new type

newtype Sum a = Sum {getSum :: a}

instance Num a => Semigroup (Sum a) where
  (Sum a) <> (Sum b) = Sum (a + b)

instance Num a => Monoid (Sum a) where
  mempty = Sum 0

𝝺> (Sum 7) <> (Sum 4)
Sum {getSum = 11}

WHY?!

Great question. Why should we jump through the hoops of defining another type for addition?!

1. Abstraction. Remember, monoids let us separate the aggregation part of a fold. This is useful because we only need to define <> for a new type and we can immediately fold e.g. over lists, trees, and anything that's foldable.
2. Semigroups give us associativity, which we can use to our advantage. For example, we can evaluate large expressions of <> in any order. This means, for example, that we can execute huge folds in a distributed fashion:

Assume that <> is an operation that is much more expensive than a simple +, then we can execute the first (...) on a different process/device and accumulate afterwards without having to worry about correctness.

(a <> b <> c) <> (d <> e <> f)

Simple examples of monoids

Any (resp. All) is the disjunctive (resp. conjunctive) monoid on Bool:

𝝺> (Any False) <> (Any True) <> (Any False)
Any {getAny = True}

For a monoid m its dual monoid is Dual m

𝝺> (Dual "a") <> (Dual "b") <> (Dual "c")
Dual {getDual = "cba"}

Product of monoids:

𝝺> (Sum 2,Product 3) <> (Sum 5,Product 7)
(Sum {getSum = 7},Product {getProduct = 21})

Advanced examples of monoids

Map is a monoid under union:

𝝺> Map.fromList [(1,"a")] <> Map.fromList [(1,"b")] <> Map.fromList [(2,"c")]
fromList [(1,"a"),(2,"c")]

where <> = Map.union is a left-biased union of keys (meaning, the left-most argument with the same key will override the ones further to the right).

We could implement another monoid instance for Map, which instead of overwriting recurring keys, accumulates the corresponding values. For this we need a new type we can call MMap:

newtype MMap k v = MMap (Map.Map k v)

fromList :: Ord k => [(k,v)] -> MMap k v
fromList xs = MMap (Map.fromList xs)

instance (Ord k, Monoid v) => Semigroup (MMap k v) where
  (MMap m1) <> (MMap m2) = MMap (Map.unionWith mappend m1 m2)

By defining <> via the unionWith function and mappend (monoidal append) we can accumulate any MMap that has values which are instances of Monoid:

𝝺> fromList [(1,"a")] <> fromList [(1,"b")] <> fromList [(2,"c")]
MMap (
 1 : "ab"
 2 : "c"
)

𝝺> fromList [('a', Sum 1)] <> fromList [('a',Sum 2)] <> fromList [('b',Sum 3)]
MMap (
 'a' : Sum {getSum = 3}
 'b' : Sum {getSum = 3}
)

The Monoid typeclass also defines the mconcat helper function

mconcat = foldr (<>) mempty

allowing us to combine any number of monoids simply by wrapping them in a list.

𝝺> mconcat [Sum 1, Sum 2, Sum 3, Sum 4]
Sum {getSum = 10}

Traversal: Foldables

With Monoid we have successfully abstracted away the aggregation part of folding operations. Now we have to formalize how to traverse datastructures we want to fold.

Let $M=⟨M,\diamond ,u⟩$ be a monoid, $f:A\to M$ a function that takes a values of type $A$ to a monoid, and lst = [a1, ... , an] a list of elements from $A$. The function foldMap of lst w.r.t. $M$ and $f$ is the composition of map f followed by the aggregation $\diamond$.

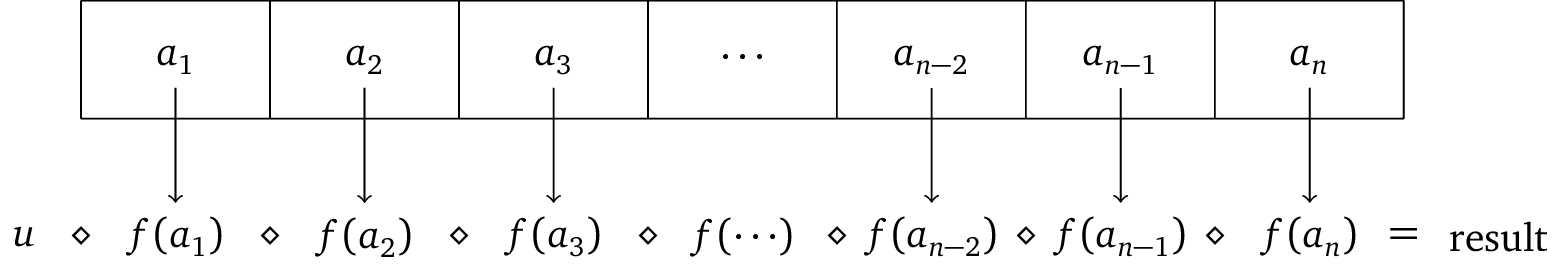
To make something Foldable, we only have to implement foldMap ^[1]:

instance Foldable [] where
  foldMap f = mconcat . map f

and we will get a lot of functions for free (including length, elem, maximum, etc.)

𝝺> :i Foldable
type Foldable :: (* -> *) -> Constraint
class Foldable t where
  fold :: Monoid m => t m -> m
  foldMap :: Monoid m => (a -> m) -> t a -> m
  foldMap' :: Monoid m => (a -> m) -> t a -> m
  foldr :: (a -> b -> b) -> b -> t a -> b
  foldr' :: (a -> b -> b) -> b -> t a -> b
  foldl :: (b -> a -> b) -> b -> t a -> b
  foldl' :: (b -> a -> b) -> b -> t a -> b
  foldr1 :: (a -> a -> a) -> t a -> a
  foldl1 :: (a -> a -> a) -> t a -> a
  toList :: t a -> [a]
  null :: t a -> Bool
  length :: t a -> Int
  elem :: Eq a => a -> t a -> Bool
  maximum :: Ord a => t a -> a
  minimum :: Ord a => t a -> a
  sum :: Num a => t a -> a
  product :: Num a => t a -> a
  {-# MINIMAL foldMap | foldr #-}
        -- Defined in ‘Data.Foldable’
instance Foldable (Either a) -- Defined in ‘Data.Foldable’
instance Foldable [] -- Defined in ‘Data.Foldable’
instance Foldable Maybe -- Defined in ‘Data.Foldable’
instance Foldable Solo -- Defined in ‘Data.Foldable’
instance Foldable ((,) a) -- Defined in ‘Data.Foldable’

For new types like Tree a we have to implement foldMap to inform Haskell about how to traverse it. For a tree we can define

data Tree a = Leaf a | Node (Tree a) (Tree a)

instance Foldable Tree where
  foldMap :: Monoid m => (a -> m) -> Tree a -> m
  foldMap f (Leaf x) = f x
  foldMap f (Node l r) = foldMap f l <> foldMap f r

tree :: Tree Int
tree = Node (Leaf 7) (Node (Leaf 2) (Leaf 3))

𝝺> foldMap Sum tree
Sum {getSum = 12}

which immediately lets us fold any Tree m where Monoid m => Tree m.

Example: MMap statistics

For MMaps we already have a monoid instance, so let's use it to compute some statistics. With a simple Count monoid we can compute how many elements of a given value are in a list:

instance Semigroup Count where
  (Count n1) <> (Count n2) = Count (n1+n2)

instance Monoid Count where
  mempty = Count 0

count :: a -> Count
count _ = Count 1

singleton :: k -> v -> MMap k v
singleton k v = MMap (Map.singleton k v)

𝝺> foldMap (\x -> singleton x (count x)) [1,2,3,3,2,4,5,5,5]
MMap (
 1 : Count 1
 2 : Count 2
 3 : Count 2
 4 : Count 1
 5 : Count 3
)

Perhaps more interestingly, we can use a product of monoids (i.e. a tuple of monoids) to compute statistics over the first letter of a list of words:

ws = words $ map toLower "Size matters not. Look at me. Judge me by my size, do you? Hmm? Hmm. And well you should not. For my ally is the Force, and a powerful ally it is. Life creates it, makes it grow. Its energy surrounds us and binds us. Luminous beings are we, not this crude matter. You must feel the Force around you; here, between you, me, the tree, the rock, everywhere, yes. Even between the land and the ship."
it :: [String]

We can define a function that collects a bunch of monoids which we want to fold over:

stats :: Foldable t => t a -> (Count, Min Int, Max Int)
stats word = (count word, Min $ length word, Max $ length word)

𝝺> stats "size"
(Count 1,Min 4,Max 4)

Each of the monoids above we want to again fold over MMaps with the first character as keys. Effectively MMap is very similar to grouping, hence the name groupBy:

groupBy :: (Ord k, Monoid m) => (a -> k) -> (a -> m) -> (a -> MMap k m)
groupBy keyf valuef a = singleton (keyf a) (valuef a)

𝝺> groupBy head stats "size"
MMap (
 's' : (Count 1,Min 4,Max 4)
)

Finally we just have to call foldMap to accumulate all the stats.

𝝺> foldMap (groupBy head stats) ws
MMap (
 'a' : (Count 10, Min 1, Max  6)
 'b' : (Count  5, Min 2, Max  7)
 'c' : (Count  2, Min 5, Max  7)
 'd' : (Count  1, Min 2, Max  2)
 ...
 'w' : (Count  2, Min 3, Max  4)
 'y' : (Count  6, Min 3, Max  4)
)

---

1. For in depth information about Foldable implementations you can refer to the Haskell Wiki. Most importantly, it shows how to implement foldr in terms of foldMap by exploiting the monoid of self-maps. ↩︎