Typeclasses

During the last lecture we introduced ad-hoc polymorphism via typeclasses. For examples, we learnt about Eq, which gave us a way to implement the equality operator == for any type. Haskell makes extensive use of typeclasses to define many kinds of abstractions and common behaviours over types. Some of the most important builtin typeclasses are shown in the diagram below.

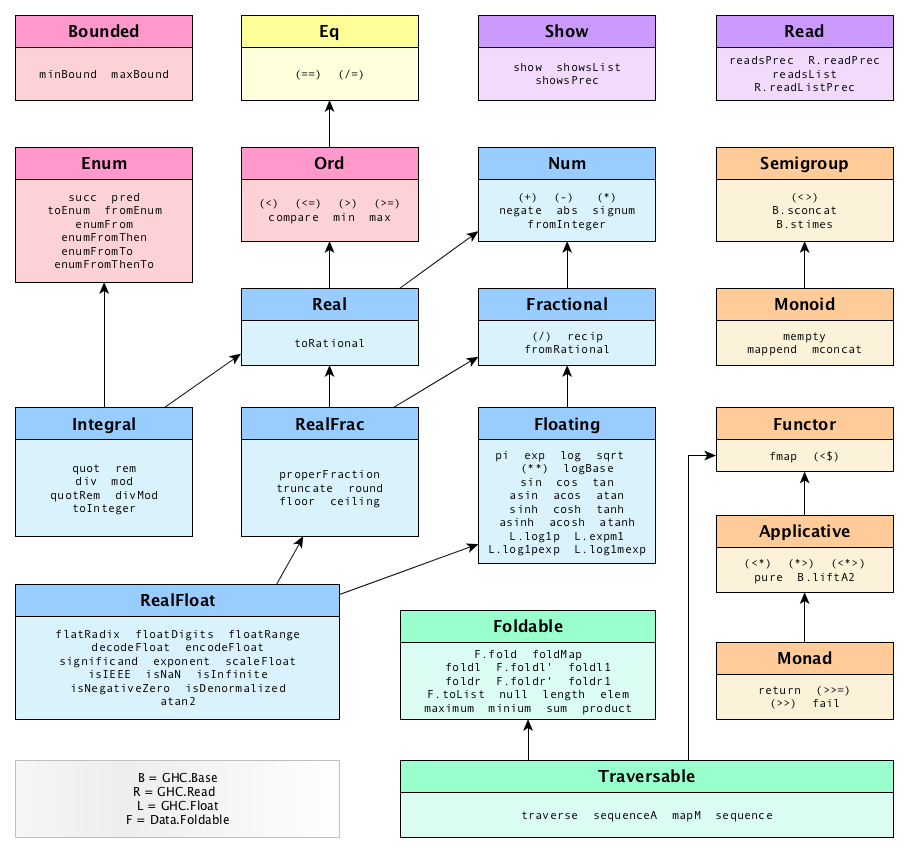
We have so far heard about Eq, Ord, Show, and Num. Today, as a warmup, we will discuss another common typeclass (Read) before starting to dive into the depths of the first really interesting Haskell typeclass, the Functor.

Read

Read is the typeclass that complements Show. It allows to parse strings into values for all instances of Read via the function

read :: Read a => String -> a

The function read is polymorphic and will typically infer the correct type to be read, but sometimes we need an explicit type annotation:

𝝺> read "3" -- fails

𝝺> read "3" :: Int
3

𝝺> read "[1,2,3]" :: [Float]
[1.0, 2.0, 3.0]

For the purposes of this course, this is all you need to know about the Read instance, but if you would like to see an implementation of and instance Read in action, take a look at the Time below.

Instance of Read for a custom Time type.

We can define a custom Time type for which we can implement the Show instance as usual

import Data.Char (isDigit)

data Time = Time {hour :: Int,
                  minute :: Int }

instance Show Time where
  show (Time hour minute) = hh ++ ":" ++ mm where
    hh = if hour > 9 then (show hour) else ("0" ++ show hour)
    mm = if minute > 9 then (show minute) else ("0" ++ show minute)

-- construct new times only if they are valid
newTime :: Int -> Int -> Time
newTime h m | between 0 23 h && between 0 59 m = Time h m
            | otherwise = error "newTime: hours must be in range 0-23 and minutes 0-59"
     where between low high val = low <= val && val <= high

𝝺> newTime 3 14
03:14

𝝺> newTime 25 0
*** Exception: newTime: hours must be in range 0-23 and minutes 0-59

To read times from a string we can define:

instance Read Time where
  readsPrec _ (h1:h2:':':m1:m2 : therest) =
    let hour   = read [h1,h2] :: Int  -- lazily doesn't get evaluated unless valid
        minute = read [m1,m2] :: Int
        in
      if all isDigit [h1,h2,m1,m2] then -- it looks valid
         [(newTime hour minute,therest)]
       else []                      -- don't give any parse if it was invalid
  readsPrec _ _ = []

which lets us parse times from e.g. a list of times:

𝝺> read "[23:34,23:12,03:22]" :: [Time]
[23:34,23:12,03:22]

This is a summary of this stackoverflow question.

Functor

We have already seen Haskell's version of one of the most important higher-order functions - map:

map :: (a -> b) -> [a] -> [b]

A functor describes a generalization of map to any data type that is "mappable", for example we might want to apply a function to every value of type a in a dictionary Map k a:

mapMap :: (a -> b) -> Map k a -> Map k b

or to every node in a Tree a:

treeMap :: (a -> b) -> Tree a -> Tree b

All these maps have in common that they preserve the structure of the data type that we map over, i.e. a list stays a list, a tree stays a tree, etc. This preservation of structure is the reason they are called functors, which is a term coming from category theory. To make something an instance of Functor you have to implement the class:

class Functor f where
  fmap :: (a -> b) -> f a -> f b

The list functor

For lists [] the function fmap is just regular old map:

instance Functor [] where
  fmap = map

More concretely, imagine you are given a data type Tree a:

data Tree a = Tree a [Tree a] deriving Show

consisting of nodes of type a and children of type [Tree a]^[1]:

tree :: Tree Int
tree = Tree 1 [Tree 2 [Tree 3 []], Tree 4 []]

A trivial operation we might want to perform with this tree is to apply (+1) to every node.

𝝺> addOne tree
Tree 2 [Tree 3 [Tree 4 []], Tree 5 []]

We can make Tree an instance of Functor by implementing fmap:

instance Functor Tree where
  fmap f (Tree x []) = Tree (f x) []
  fmap f (Tree x ts) = Tree (f x)
                            (map (fmap f) ts)

Now we can easily define functions that operate on the node values of our tree, such as addOne:

addOne :: (Num a) => Tree a -> Tree a
addOne tree = fmap (+1) tree

𝝺> addOne tree
Tree 2 [Tree 3 [Tree 4 []],Tree 5 []]

Generalization of addOne

The power of our Functor definition comes is when we allow addOne to be applied more generally to any Functor f:

addOne :: (Functor f, Num a) => f a -> f a
addOne = fmap (+1)

Without writing any additional code we have implemented addOne for any functor, and things immediately work:

𝝺> addOne [1,2,3]
[2,3,4]

𝝺> addOne (Map.fromList [('a',1), ('b',2)])
Map.fromList [('a',2), ('b',3)]

Kinds of types

To figure out what kinds of types we can implement Functor for, we have to look at which arguments Functor accepts. But Functor is a type constructor... How do we look at the type of a type constructor...?

In Haskell, "types" of types, are called kinds, and we can inspect them via :kind:

𝝺> :kind Int
Int :: *

𝝺> :kind Char
Char :: *

We see that Int and Char have the kind *, and so does every other type that we would use as a classic type for a value. Things become interesting when we look at e.g. the type of e.g. Tree:

𝝺> :kind Tree
Tree :: * -> *

which tells us that Tree has the kind * -> *, so it accepts a type of kind * and creates a new type. Concretely, Tree Int accepts an Int and produces a type Tree Int :: *. This is where the name type constructor comes from. Tree is essentially a function on types. The same is true for example for lists:

𝝺> :k []
[] :: * -> *

So, what can we learn from the kind of Functor?

𝝺> :k Functor
Functor :: (* -> *) -> Constraint

A Functor accepts a function form one kind to another * -> * (i.e. a type constructor) and produces a Constraint. So we can pass e.g. a Tree :: * -> * to Functor to produce the constraint Functor Tree. Constraints are the type constrains we know from the beginning of our type signatures, such as (+) :: (Num a) => a -> a -> a. Hence we can pass any type constructor of a single type to Functor, like we did with Tree:

instance Functor Tree where
  ...

because Tree :: * -> *. If we have a type constructor with multiple arguments, such as a dictionary Map k a, we can make it functorial for only one argument. Currying works for type constructors as well, so we could just define:

instance Functor (Map k) where
  ...

to make Map k a functorial in a, which is exactly how fmap works for Haskell's Maps. Applying fmap to a Map leaves the keys k unchanged and applies the function to the values a:

fmap :: (a -> b) -> Map k a -> Map k b

𝝺> fmap (+1) (Map.fromList [('a',5), ('b',6)])
fromList [('a',6), ('b',7)]

Hack: Functoriality in arguments other than the last.

If we have a type constructor MyType a b in which we want to implement fmap for the argument a we would intuitively like to write something like:

instance Functor (\b -> MyType a b) where
    fmap f (MyConstructor x y) = MyConstructor (f x) y

which is unfortunately not syntactically correct Haskell, we just can't write lambdas in instance declarations this way. Instead we can use newtype:

newtype MyTypeFunctor b a = MyTypeFunctor (MyType a b)

instance Functor (MyTypeFunctor b) where
    fmap f (MyTypeFunctor (MyConstructor x y)) = MyTypeFunctor (MyConstructor (f x) y)

Safe computations

Haskell prides itself with its ability to write safe but still high-level code. Equipped with our understanding of Functors we can take a first step towards handling errors in pure code.

To define safe operations in Haskell, we can use

data Maybe a = Nothing | Just a

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead xs = Just (head xs)

safeTail :: [a] -> Maybe [a]
safeTail [] = Nothing
safeTail (_:xs) = Just xs

which will let us get the head and tail of empty lists without unrecoverably failing:

𝝺> safeHead [1,2,3]
Just 1

𝝺> safeHead []
Nothing

𝝺> head []
*** Exception: Prelude.head: empty list

We obviously will want to compose functions like safeHead and e.g. (+1), but we will run into a problem: (+1) :: (Num a) => a -> a does not accept Maybe a! A solution would be:

add1Maybe :: Maybe Int -> Maybe Int
add1Maybe Nothing = Nothing
add1Maybe (Just n) = Just (n + 1)

But that is not scalable. We would have to implement this pattern for any new function a -> a! What we need is a function that does the following:

(a -> b) -> Maybe a -> Maybe b

and in fact, this is exactly what we were doing with addOne = fmap (+1) before (the type signature above is just fmap for Maybe). The function addOne has the signature

addOne :: (Functor f) => f a -> f b

so we can immediately compose it with safeHead:

safeAdd1ToHead :: Maybe Int -> Maybe Int
safeAdd1ToHead  = addOne . safeHead

𝝺> safeAdd1ToHead [1,0,0]
Just 2

𝝺> safeAdd1ToHead []
Nothing

This works, because Maybe is already an instance of Functor:

instance Functor Maybe where
    fmap _ Nothing = Nothing
    fmap f (Just x) = Just (f x)

Composing failing computations

We can operate with functions on Maybes. But what if we would like to compose functions that outputs Maybes, such as the safe equivalent of second = head . tail? We cannot just write

safeSecond :: [a] -> Maybe a
safeSecond = safeHead . safeTail

because safeHead does not accept a Maybe [a]... We could again do it manually for every function we would like to compose:

safeSecond :: [a] -> Maybe a
safeSecond xs =
  let xs' = safeTail xs
  in case xs' of
    Nothing -> Nothing
    Just xs'' -> safeHead xs''

But this does not scale at all:

safeFourth :: [a] -> Maybe a
safeFourth xs =
  let xs' = safeTail xs
  in case xs' of
    Nothing -> Nothing
    Just xs1 ->
      let xs1' = safeTail xs1
      in case xs1' of
        Nothing -> Nothing
        Just xs2 ->
          let xs2' = safeTail xs2
          in case xs2' of
            Nothing -> Nothing
            Just xs3 -> safeHead xs3

Instead we can extract this pattern and write a glue function andThen for it:

andThen :: Maybe a -> (a -> Maybe b) -> Maybe b
andThen Nothing _ = Nothing
andThen (Just x) f = f x

We will discuss this pattern much more in future lectures. It is known as a Monad and puts another very powerful tool into our box of Haskell goodies:

safeSecond :: [a] -> Maybe a
safeSecond xs = safeTail xs `andThen` safeHead

safeFourth :: [a] -> Maybe a safeFourth xs =
  safeTail xs `andThen`
  safeTail `andThen`
  safeTail `andThen`
  safeHead

Either

You can implement error message handling with the same pattern we used above with the type Either. It is very similar to Maybe, just that it has a second value that can actually contain something (like an error message):

data Either a b = Left a | Right b

We could, for example, implement a safe division that reports and error:

safeDiv :: Int -> Int -> Either String Int
safeDiv _ 0 = Left "Division by 0 error"
safeDiv x y = Right (x `div` y)

and compose computations in the same manner as done for Maybe. Either has two parameters so its kind is * -> * -> *. Hence, we have to be careful how we implement Functor for it (remember Functor accepts * -> *), just like we have to do a little bit of thinking for andThen, but that is an exercise for the next lectures.

---

1. In Tree a, the empty list [] naturally denotes the end of the tree. ↩︎