Lab 7: Lambda calculus

This lab focuses on lambda calculus. First, we focus on the syntax of -expressions. Second, we focus on its semantics, i.e., the computation specified by -expressions whose one step is performed by the -reduction (and -conversion if necessary). To help you to play with these notions and concepts, I implemented in Racket an interpreter of -calculus transforming a given -expression into its normal form (if it exists). It follows the normal order evaluation strategy. In addition, I implemented a few helpers functions to help you inspect -expressions. You can download the interpreter: lambda-calculus.rkt

To follow the exercises, it is recommended to have a piece of paper, a pen, DrRacket IDE installed, and the interpreter. To use the interpreter, download the above-mentioned file and store it in a directory where you want to create your own code. Then create a new Racket file starting as follows:

#lang racket
(require "lambda-calculus.rkt")

-expressions are represented in the interpreter as S-expressions. It does not allow to use of any conventions regarding parenthesis. So you need to place them all explicitly. For instance, the -expression has to be represented as follows:

'(λ x : (λ y : ((x y) (λ a : (λ b : b)))))

So we had to add the outermost parenthesis, expand the shortcuts to , and put the parenthesis determining the order of the applications, i.e., as the application is left-associative, is in fact . The symbol λ can be entered in DrRacket by pressing Ctrl+\. Instead of the dot symbol, the colon symbol is used.

The module lambda-calculus.rkt provides the following functions:

Function	Description
(draw-expr expr)	draws the syntax tree the given -expression expr; redexes are colored in red
(substitute expr var val)	substitutes val for the free occurrences of var in expr
(reduce expr)	reduces expr by a one-step -reduction in the normal order
(eval expr [info 'quiet])	finds the normal form of expr; if info is set to 'verbose, displays all the steps; if info is 'tree, then all the steps are drawn as trees

Exercise 1

Draw the syntax tree of the -expression and determine which variable occurrences are free and which are bound.

We will use the helper function draw-expr. First, create the correct representation as an S-expression:

'((λ x : (y (x x))) (λ y : (y (x x))))

Then evaluate the following function call:

(draw-expr '((λ x : (y (x x))) (λ y : (y (x x)))))

Displays the tree below: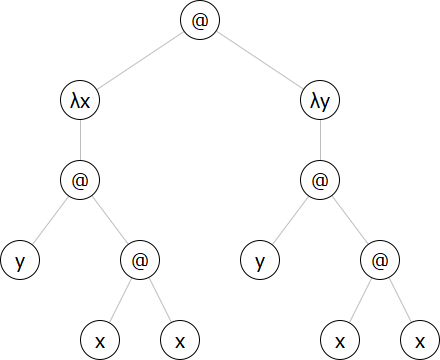

An occurrence of a variable is bound if it is in the syntax tree below the node and is free otherwise. So, for our expression, the occurrences of in the left branch are bound, and they are free in the right branch. The occurrence of in the left branch is free and bound in the right branch.

Exercise 2

Draw the syntax tree of the -expression and determine which variable occurrences are free and which are bound.

Try first to draw the tree on paper. Then compare your result with the result returned by the function draw-expr. The -expression is represented in Racket as follows:

'(λ y : ((x y) (λ a : (λ b : b))))

Exercise 3

Find all redexes in . Which one is the leftmost outermost redex, and which is the leftmost innermost redex? Reduce the leftmost outermost redex.

Hint

Try to find the redexes. Then call (draw-expr expr) for expr being the following S-expression:

'(((λ x : (x y)) z) ((λ u : u) ((λ v : v) z)))

The roots of redexes are colored red. To check that your reduction was correct, call

(reduce '(((λ x : (x y)) z) ((λ u : u) ((λ v : v) z))))

Exercise 4

Recall that multiplication of two numbers is computed by

Find the normal form of following the normal order reduction strategy, i.e., compute , which should result in . The numbers are abbreviations for -expressions and respectively.

Hint

Once you do it on paper, check your result in Racket. You can use Racket definitions and semiquoting to make your -expression more readable.

(define zero '(λ s : (λ z : z)))
(define one '(λ s : (λ z : (s z))))
(define M '(λ a : (λ b : (λ c : (a (b c))))))

(eval `((,M ,zero) ,one) 'verbose)  ; displays each reduction step as λ-expression
(eval `((,M ,zero) ,one) 'tree)     ; draws each reduction step as syntax tree

Exercise 5

Recall that a pair is represented in -calculus as

The projections into the first and second components can be obtained by applying to Boolean values and . Thus

We can even define a cons function by . In Racket, you can define all these constructions as follows (the final two calls check that it behaves as expected):

(define T '(λ x : (λ y : x)))
(define F '(λ x : (λ y : y)))

(define CONS
  '(λ a : (λ b : (λ z : ((z a) b)))))

(eval `(((,CONS a) b) ,T))
(eval `(((,CONS a) b) ,F))

Write a -expression swapping components of a given pair .

Hint

The desired -expression should take a pair and return another pair with swapped components. So the expression should start with where the question marks are the components of the returned pair.

Solution

Once you have it, define SWAP and check that it correctly swaps the components:

(eval `(,SWAP ((,CONS a) b))) => '(λ z : ((z b) a))

Solution

(define SWAP `(λ p : (λ z : ((z (p ,F)) (p ,T)))))

Exercise 6

Since we can create pairs, we can create lists as in Racket. We represent the empty list by the false value . Now we can create a list '(a b) by

(define lst `((,CONS a) ((,CONS b) ,F)))

(eval `(,lst ,T))  => 'a
(eval `((,lst ,F) ,T)) => 'b

Write a -expression testing if a list is empty, i.e., it returns if it is empty and otherwise.

Hint

A list is either a pair or if it is empty. Let denote it by . Recall the definition of the zero test from the lecture

where . We need something similar for the list . So our desired -expression should look like where have to be filled by suitable -expressions serving as arguments for . If is empty (i.e., ), then is just a projection into the second argument. Thus should be , i.e., we have . If we substitute for a pair (i.e. ), we obtain . Thus is going to be substituted for , and consequently, it will be applied to and , i.e., we would end up with . Since the result in this case should be , we need the result of to be because .

Solution

Check your solution in Racket.

Code

(define neg `(λ x : ((x ,F) ,T)))
(define NULL? `(λ p : ((p (λ a : (λ b : ,neg))) ,T)))

(eval `(,NULL? ,F)) ; => T
(eval `(,NULL? ,lst)) ; => F

Exercise 7

Define a -expression computing the length of a list.

Hint

Follow the approach from the lecture where we defined a function

which we turned into a recursive one by -combinator (i.e., ).

Recall:

You also need the successor function

for adding . The computation of the desired -expression can be expressed in Racket as follows:

(define len
  (lambda (p) (if (null? p)
                    0
                    (+ (len (cdr p)) 1))))

Modify the -expression by replacing with from the previous exercise. Adding can be done by applying the successor function , and the predecessor function must be replaced by the expression returning the second component.

Solution

Check your solution in Racket:

Code

(define S '(λ w : (λ y : (λ x : (y ((w y) x))))))
(define Y '(λ y : ((λ x : (y (x x))) (λ x : (y (x x))))))

(define LEN
  `(λ r :
     (λ lst : (
               ((,NULL? lst) ,zero)
               (,S (r (lst ,F)))))))

(eval `((,Y ,LEN) ,F)) ; => 0
(eval `((,Y ,LEN) ((,CONS a) ,F))) ; => 1
(eval `((,Y ,LEN) ((,CONS a) ((,CONS b) ,F)))) ; => 2