List of Main Exam Tasks

The Main Exam Tasks in will be variations of the tasks from the following list.

Building Trees

In this task, you will build a tree from an intial tree and a sequence of edges. Your task is to iterate through the edge sequence from left to right and expand successively the initial tree. Each edge is a pair $(s,t)$. To expand the tree by the edge $(s,t)$, you must traverse through the tree and locate the node $s$. Next, you add $t$ among its children. If $s$ does not occur in the tree, the edge is ignored.

For example, suppose that the initial tree is just a single node (a leaf) $1$ and the edge sequence equals $(1,2),(1,3),(5,7),(2,4),(4,5),(3,6)$. By expanding the initial tree by the edges, we obtain the following sequence of trees:

Note that the third edge $(5,7)$ was ignored because there is no node $5$ in the currently constructed tree. So the currently constructed tree remains unchanged.

Cheap Flights

In this task your goal is to find the cheapest flights from one airport to another. You are given an undirected graph that is represented by a list of nodes (airports) and a list of edges (connections from airport to airport). Each edge contains the two nodes that it connects as well as the cost of traveling along the edge.

Below you can see an exemplary graph with 5 nodes. The cost to travel along an edge is written next to the corresponding edge.

Convex Hull

The convex hull of a set of points is the smallest convex shape that contains the whole set. Fig. 1A shows a set of six points - five of which constitute the \emph{generating points} of their convex hull. In this task you have to find smallest set of generating points of the convex hull of a given set of points.

Figure 1

.

(A): Convex hull of a set of points depicted by the dashed line. The generating points in counter-clockwise order are: $P$, $A$, $B$, $C$, $D$.

(B): Three of the polar angles ${\phi }_i$ that have to be computed to sort the points.

Fermat Primality Test

In this task, for a given natural number $p$

1. generate a sequence of pseudorandom natural numbers $a$ such that $2\le a<p-1$,
2. test whether $p$ is prime by checking whether the following equation holds for each generated pseudorandom number $a$

$$a^{p-1}\equiv 1(\mathtt{\text{mod }}p).$$

If $(2)$ holds for all numbers $a$, it is highly probable that $p$ is prime. This probabilistic primality test is known as the Fermat Primality Test. Note, the Carmichael numbers, which are composite yet pass the test for all $a$ relatively prime to the respective number, are avoided when testing your implementation of this task.

Pseudo-random Number Generation

To generate pseudorandom numbers in a given interval, use the Linear Congruential Generator (LCG)

$$x_{n+1}=(A{x}_n+C)\mathtt{\text{mod}}M,$$

where $A$, $C$ and $M$ are constants. This equation generates the next pseudorandom number $x_{n+1}$ from the previous $x_n$. The number $x_0$ is the seed.

The number $b$ drawn from $(1)$ can be transformed to the interval $b^{\text{lower}}\le b^{\prime }<b^{\text{upper}}$ as

$$b^{\prime }=(b\mathtt{\text{mod}}(b^{\text{upper}}-b^{\text{lower}}))+b^{\text{lower}}.$$

Filetree

A filetree can be used to efficiently search/replace in large filesystems. You can think of it as a tree with a variable size of nodes.

You are given a list of files (directories separated by /) like this:

src/tree.hs
src/complex.hs
scripts/ex1/test.ss
scripts/ex1/eval.ss
scripts/emptydir
scripts/ex2/test.ss
tests/test_tree.hs

Implement a function which converts the list of files into a tree, and a second function check if a file or directory is already in the tree.

Non-deterministic Finite Automata

In the seminars, we have encountered Deterministic Finite Automata (DFAs). In this task, we will work with a generalized version of the DFA that is called Non-deterministic Finite Automaton (NFA). NFA is the 5-tuple

• set of states $\mathcal{Q}$,
• a finite set of input symbols $\mathrm{\Sigma }$ (called alphabet),
• a set of transitions $\mathrm{\Delta }\subseteq \mathcal{Q}\times \mathrm{\Sigma }\times \mathcal{Q}$,
• a start state $q_0$,
• a set of final states $\mathcal{F}\subseteq \mathcal{Q}$.

In other words, NFA is just a directed graph whose vertices are states and transitions are edges labelled by symbols from $\mathrm{\Sigma }$, i.e., if $(s,a,t)\in \mathrm{\Delta }$ then there is an edge leading from the state $s$ to the state $t$ labelled by $a\in \mathrm{\Sigma }$. We say that NFA accepts a word $w=a_1{a}_2\dots a_n\in {\mathrm{\Sigma }}^{\ast }$ (i.e., a finite sequence of symbols form $\mathrm{\Sigma }$) if there exists a path leading from the start state into a final one labelled consecutively by symbols $a_1,a_2,\dots ,a_n$.

An example of an NFA is depicted in the figure below. This NFA accepts e.g. words $abb$ or $aba$. On the other hand, it accept neither $ba$ nor $abab$.

Example of NFA where $\mathcal{Q}=\{1,2,3,4\}$, $\mathrm{\Sigma }=\{a,b\}$, $q_0=1$, $\mathcal{F}=\{2,3\}$ and $\mathrm{\Delta }=\{(1,a,2),(2,b,2),(1,a,3),(3,b,4),(4,a,3),(2,a,4)\}$.

Text Justification

Given an array of strings words and a width maxWidth, format the text such that each line has exactly maxWidth characters and is fully (left and right) justified.

You should pack your words in a greedy approach; that is, pack as many words as you can in each line. Pad extra spaces ' ' when necessary so that each line has exactly maxWidth characters.

Extra spaces between words should be distributed as evenly as possible. If the number of spaces on a line does not divide evenly between words, the empty slots on the left will be assigned more spaces than the slots on the right.

For the last line of text, it should be left-justified, and no extra space is inserted between words.

Least Common Ancestor

Suppose we have a binary tree $t$. For any two nodes $x,y$ in the tree $t$, the least common ancestor of $x$ and $y$ is defined as the node $z$ satisfying the following two conditions:

1. $x$ and $y$ are descendants of $z$,
2. if there is a node $z^{\prime }$ having $x$ and $y$ as descendants, then $z$ is descendant of $z^{\prime }$.

To find the least common ancestor of two nodes $x$ and $y$ in a tree $t$, we follow the steps below:

1. find the path $p_x$ from the root $r$ of $t$ to $x$ (i.e., a list of nodes starting in $r$ and ending in $x$),
2. find the path $p_y$ from $r$ to $y$,
3. consider the common prefix of $p_x$ and $p_y$, the last node in the common prefix is the least common ancestor.

Consider, for example, the binary tree depicted below. The least common ancestor of $3$ and $5$ is $2$. Indeed, the path from the root $1$ to $3$ is $1,2,3$. The path from $1$ to $5$ is $1,2,4,5$. Their common prefix is $1,2$ whose last element is $2$.

Similarly, the least common ancestor of $5$ and $8$ is $1$. The least common ancestor of $7$ and $7$ is $7$.

Manhattan Distance

Suppose we have a list of named coordinates:

(define points
 '((#\A 1 1)
   (#\B 1 6)
   (#\C 8 3)
   (#\D 3 4)
   (#\E 5 5)
   (#\F 8 9)))

They can be printed on a 2D grid (with dimensions according to the largest x and y coordinates, and (0, 0) on the top left)

.........
.A.......
.........
........C
...D.....
.....E...
.B.......
.........
.........
........F

Your task is to fill each . with the lower case letter of the closest coordinate according to the Manhattan distance. We call the resulting grid the nearest-neighbour grid.

aaaaa.ccc
aAaaa.ccc
aaaddeccc
aadddeccC
..dDdeecc
bb.deEeec
bBb.eeee.
bbb.eeeff
bbb.eefff
bbb.ffffF

The grid points which still contain a . represent tied points, i.e. points which have at least two equally close neighbours. The Manhattan distance between two points is defined by

$$d=|x_1-x_2|+|y_1-y_2|$$

Minesweeper

Implement a program to mark the number of mines directy adjacent (horizontally, vertically and diagonally) to squares on a rectangular Minesweeper field.

Fields with . denote an empty field and * denote mines:

.*.*.
..*..
..*..
.....

Your program should output the following

1*3*1
13*31
.2*2.
.111.

Minimum Spanning Tree

Given a connected weighted graph $G=(V,E)$ with a weight function $w:E\to \mathbf{N}$ assigning to each edge $e$ its weight $w(e)$, its minimum spanning tree is a graph $T=(V,E^{\prime })$ such that $E^{\prime }\subseteq E$, $T$ is a tree (i.e., a connected graph without cycles) and $\sum _{e\in E^{\prime }}w(e)$ is minimum possible among such trees. The figure shows an example of a connected weighted graph and its minimum spanning tree.

Your task is to implement an algorithm computing the minimum spanning tree, i.e., a function returning for a given connected weighted graph $(V,E)$ the subset $E^{\prime }$ of edges in the minimum spanning tree.

$N^2$-Knights

In chess, a knight can move to any square that is two squares away horizontally and one square away vertically, or two squares vertically and one square horizontally. Therefore, its complete move looks like the letter "L".

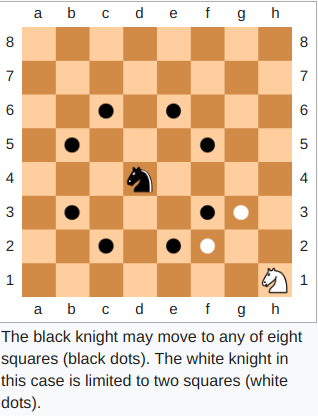
The $N^2$-knights puzzle concerns placing $O(N^2)$ knights on an $n\times n$ chessboard so that no two knights can attack each other. Below, you can see a valid configuration for a 8x8 board.

Determine the validity of $N^2$-knights board configurations.

Photographing Skyscrapers

You are an avid photographer that is obsessed with regular structures and you want to take pictures of cities that are built on regular grids. It turns out that you are also really into roof tops so you want to see as many of them in your pictures as possible. Naturally, you wonder from which side of a given city (North/South/East/West) you should be taking the picture. Luckily a befriended architect gave you maps of the cities you want to photograph. The maps are very simplified and can be represented as lists of lists of integers, so for example in Scheme:

;    north
(define city
  '((3 0 3 7 3)
    (2 5 5 1 2)
    (6 5 3 3 2)
    (3 3 5 4 9)
    (3 5 3 9 0)))
;    south

Every number represents the height of a building.

A roof is visible if all other roofs between it and the edge of the grid are smaller than it. Only consider roofs in the same row or column. The first roof at the edge of a grid is always visible.

Pretty Printing of Binary Numbers

The goal of this assignment is to implement a program that reads a positive integer from standard input, converts it into its binary representation, and displays this representation as a text image. Each digit (i.e., $0$ and $1$) is represented as a $4\times 4$ grid of characters.

Implement a program that works as follows:

1. Display a message Enter integer:.
2. Let the user enter an integer $n$ (you may assume only valid inputs).
3. Convert $n$ into its binary representation.
4. Display the binary representation using the above text-images. The particular digits must be separated by a column consisting of the character '.'.

Below you can see an example run were the user enters the number 12.

Enter integer:
12
...#....#..##...##.
..##...##.#..#.#..#
...#....#.#..#.#..#
...#....#..##...##.

Multiplayer Rock, Paper, Scissors

Determine the winner (or remaining players) after several rounds of multiplayer Rock, Paper, Scissors.

Players stand in a circle and all throw at once. If rock, paper, and scissors are all thrown, it is a stalemate, and they rethrow. If only two throws are present, all players with the losing throw are eliminated. The following function decides which throws from a set of set of throws in a single round should be eliminated.

$$\text{eliminated}(\text{throws})\equiv \{\begin{array}{ll}\mathtt{\text{rock}}& \mathtt{\text{paper}},\mathtt{\text{rock}}=\text{throws}\\ \mathtt{\text{paper}}& \mathtt{\text{paper}},\mathtt{\text{scissors}}=\text{throws}\\ \mathtt{\text{scissors}}& \mathtt{\text{rock}},\mathtt{\text{scissors}}=\text{throws}\\ \mathrm{\varnothing }& \text{otherwise}\end{array}$$

The actions of players are decided in advance; e.g. for two rounds of three-player RPS, the players and actions are represented as:

(define players '("alice" "bob" "charlie"))
(define strategies '((r p) (r r) (s p)))

where Alice throws Rock in the first round, then Paper in the second. Charlie never gets to throw his second pick (Paper), as he will be eliminated after one round. Alice is the only remaining player after the two rounds. The result should be '("alice").

You will need to keep track of the players and their actions. In each round, figure out which throws should be eliminated, then filter out the corresponding players and their strategies. Create two helper functions: one that creates a boolean "mask" of all the winners of a single round, and one that performs the filtering.

Sierpinski Carpet

The Sierpiński carpet is a plane fractal first described by Wacław Sierpiński in 1916. Your task is to generate this fractal in a text format represented as a list of strings. Each string represents a single row in the picture. The picture $f(n)$ is defined recursively. For $n=0$, we define $f(0)=\mathtt{\text{"\#"}}$. For $n>0$, we define $f(n)$ as shown below.

In other words, $f(n)$ consists of eight copies of $f(n-1)$ and the middle box of the same size as $f(n-1)$ filled with spaces. The first iterations $f(0)$, $f(1)$, $f(2)$, and $f(3)$ look as follows:

##     ###      #########      ###########################
      # #      # ## ## #      # ## ## ## ## ## ## ## ## #
      ###      #########      ###########################
               ###   ###      ###   ######   ######   ###
               # #   # #      # #   # ## #   # ## #   # #
               ###   ###      ###   ######   ######   ###
               #########      ###########################
               # ## ## #      # ## ## ## ## ## ## ## ## #
               #########      ###########################
                              #########         #########
                              # ## ## #         # ## ## #
                              #########         #########
                              ###   ###         ###   ###
                              # #   # #         # #   # #
                              ###   ###         ###   ###
                              #########         #########
                              # ## ## #         # ## ## #
                              #########         #########
                              ###########################
                              # ## ## ## ## ## ## ## ## #
                              ###########################
                              ###   ######   ######   ###
                              # #   # ## #   # ## #   # #
                              ###   ######   ######   ###
                              ###########################
                              # ## ## ## ## ## ## ## ## #
                              ###########################

The size of the picture grows exponentially with $3^n$.

Spiral Matrix

A Spiral Matrix is a square $n\times n$-matrix filled with natural numbers, starting from $1$ in the top-left corner, increasing in inward, clockwise spiral order, like these examples:

$${\mathbf{S}}_3=\left(\begin{array}{rrr}1& 2& 3\\ 8& 9& 4\\ 7& 6& 5\end{array}\right){\mathbf{S}}_5=\left(\begin{array}{rrrrr}1& 2& 3& 4& 5\\ 16& 17& 18& 19& 6\\ 15& 24& 25& 20& 7\\ 14& 23& 22& 21& 8\\ 13& 12& 11& 10& 9\end{array}\right)$$

Even though one can define a spiral matrix for each size $n$, your task is to implement a function generating a spiral $n\times n$-matrix only for odd $n$. Note that such matrices can be generated recursively because the spiral matrix ${\mathbf{S}}_n$ of size $n\times n$ can be constructed from the spiral matrix ${\mathbf{S}}_{n-2}$ of size $(n-2)\times (n-2)$ as follows:

$${\mathbf{S}}_n=\left(\begin{array}{rrrrr}1& 2& \cdots & n-1& n\\ 4n-4& & & & n+1\\ ⋮& & \mathbf{B}& & ⋮\\ 3n-1& & & & 2n-2\\ 3n-2& 3n-3& \cdots & 2n& 2n-1\end{array}\right)$$

where $\mathbf{B}$ is basically the matrix ${\mathbf{S}}_{n-2}$ whose all elements are increased by $4n-4$.

Square Code

One classic method for composing secret messages is called a square code. First, the input is normalized: the spaces and punctuation are removed from the English text, and the message is downcased. Then, the normalized characters are broken into rows. These rows can be regarded as forming a rectangle. For example, the sentence

If man was meant to stay on the ground, god would have given us roots.

is normalized to:

ifmanwasmeanttostayonthegroundgodwouldhavegivenusroots

The normalized string is 54 characters long, so it is written into a rectangle with 7 rows and 8 columns.

  ifmanwas
  meanttos
  tayonthe
  groundgo
  dwouldha
  vegivenu
  sroots

Note that the last row is padded with spaces at the end to make it 8 characters long.

The coded message is obtained by reading down the columns going left to right. For example, the message above is coded as:

imtgdvs fearwer mayoogo anouuio ntnnlvt wttddes aohghn  sseoau

Given the length $n\in \mathbb{N}$ of the normalized text, the number of columns $c\in \mathbb{N}$ in the rectangle is computed by $c=\lceil \sqrt{n}\rceil$, i.e., $c$ is the smallest natural number greater than or equal to $\sqrt{n}$.

Unit Propagation

The Davis–Putnam–Logemann–Loveland (DPLL) algorithm is the core of SAT solvers nowadays. It takes a propositional formula in CNF (conjunctive normal form) and returns true if, and only if, the formula is satisfiable. A formula in CNF is usually represented as a set of clauses. A clause is represented as a set of literals. A literal is either a propositional variable (e.g. $x$) or its negation (e.g. $\mathrm{\neg }x$). For instance, a formula

$$\phi =(a\vee b\vee \mathrm{\neg }c\vee \mathrm{\neg }f)\wedge (b\vee c)\wedge (\mathrm{\neg }b\vee e)\wedge \mathrm{\neg }b$$

is represented as

$$\phi =\{\{a,b,\mathrm{\neg }c,\mathrm{\neg }f\},\{b,c\},\{\mathrm{\neg }b,e\},\{\mathrm{\neg }b\}\}.(1)$$

One of the subroutines of the DPLL algorithm is the unit propagation simplifying the input formula. A unit is a clause containing a single literal, e.g. $\{\mathrm{\neg }b\}$. It is obvious that a satisficing evalution for a formula in CNF must evaluate all units to true. This allows simplifying the input formula. Assume that a set of clauses $\phi =\{c_1,\dots ,c_n\}$ has a unit, i.e., $c_k=\{u\}$ for some $k$ and literal $u$, then $\phi$ can be simplified by the following rules:

1. if $u\in c_i$, then $c_i$ can be removed from $\phi$,
2. if $\mathrm{\neg }u\in c_i$, then $\mathrm{\neg }u$ can be removed from $c_i$.

For example, the formula $\phi$ in $(1)$ has a unit $\{\mathrm{\neg }b\}$, so we can simplify to $\{\{a,\mathrm{\neg }c,\mathrm{\neg }f\},\{c\}\}$. Note that by propagating the unit, a new unit was created. Thus we can continue and propagate the unit $\{c\}$ obtaining $\{\{a,\mathrm{\neg }f\}\}$. The resulting set of clauses has no unit.

Your task is to implement the unit propagation for a given formula $\phi$ in CNF, i.e., eliminate all possible unit clauses. See the following pseudocode.

while there is a unit clause |{u}| in |φ| do
      |φ| <- unit-propagate(u, |φ|);

Heap: Balanced Binary Tree

A Heap is a tree that satisfies the heap property: the node's value is greater or equal to the value of any of its children. As a result, the heap's root carries the greatest value in the heap. Hence, heaps are commonly used to implement queue-like data structures. Further, let us consider the heap as a balanced binary tree, where a binary tree is balanced if the heights of the left and right subtree of any node differ by not more than one.

Balanced binary tree fulfilling the heap property that is returned by the described algorithm.

Another valid balanced binary tree fulfilling the heap property.

Balanced binary tree violating the heap property (violating notes marked in red).

Binary tree fulfilling the heap property that is not balanced (one pair of empty subtree-endpoints violating the depth difference limit in red; note, there are additional violations that are not marked).

Your task is to implement a function that builds a heap from a given list of elements This function starts with the empty leaf, inserts elements one by one, and fixes the heap property after each insertion.